FINDING AREA OF KITE

Area of kite ?

A kite is a quadrilateral which has two pairs of adjacent sides equal in length.

To find area of kite we need diagonals.

Area of kite = (1/2) x diagonal 1 x diagonal 2

Find the area of each kite.

Problem 1 :

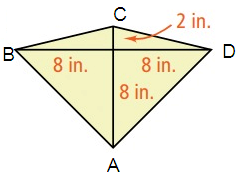
Solution :

Area of a kite = 1/2 d₁d₂

AC perpendicular BD

d₁ = 2 + 8 = 10

d₂ = 8 + 8 = 16

= 1/2 (10)(16)

= 80

So, area of a kite is 80 in².

Problem 2 :

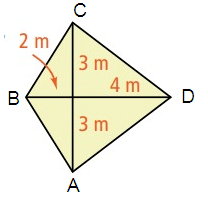
Solution :

Area of a kite = 1/2 d₁d₂

AC perpendicular BD

d₁ = 3 + 3 = 6

d₂ = 2 + 4 = 6

= 1/2 (6)(6)

= 18

So, area of a kite is 18 m².

Problem 3 :

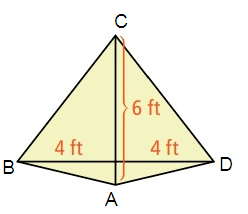
Solution :

Area of a kite = 1/2 d₁d₂

AC perpendicular BD

d₁ = 4 + 4 = 8

d₂ = 6

= 1/2 (8)(6)

= 24

So, area of a kite is 24 ft².

Problem 4 :

The area of a kite is 120 cm². The length of one diagonal is 20 cm. what is the length of the other diagonal?

a) 12cm     b) 20 cm       c) 24 cm     d) 48 cm

Solution :

Given, area of a kite is 120 cm²

Length of one diagonal d₁ = 20 cm.

Let length of the other diagonal d₂ be x.

Area of a kite = 1/2 d₁d₂

120 = 1/2 (20)(x)

120 = 10x

Divide both sides by 10.

120/10 = 10x/10

12 = x

So, length of the other diagonal is12 cm.

Problem 5 :

A kite has vertices at the points (2, 0) (3, 2) (4, 0) and (3, -3). Find the perimeter and area of the kite.

Solution :

Let the given points be A (2, 0) B (3, 2) C (4, 0) and D (3, -3)

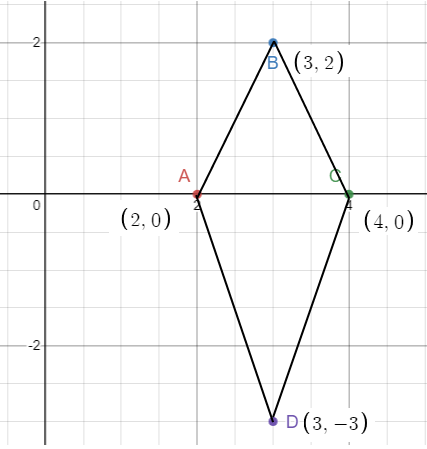
Finding area :

Area of kite = (1/2) x AC x BD

AC = 2 units

BD = 5 units

= (1/2) x 4 x 5

= 10 square units.

Finding perimeter :

To find the perimeter of the kite, we need length of all sides. To figure out the length of the sides, we may use Pythagorean theorem.

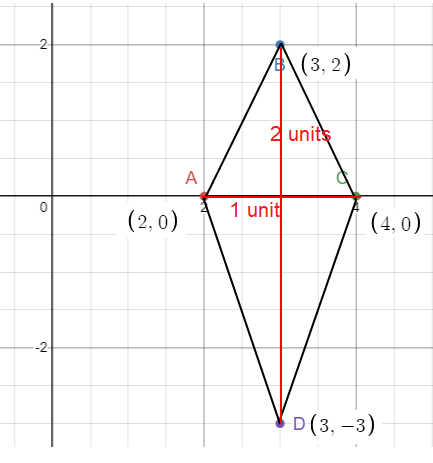
Finding Perimeter :

Let AB = x

We know that diagonals of a kite bisect each other at right angles. Let O be the point of intersection of diagonals.

Using Pythagorean theorem, we get

Perimeter of kite ABCD = 2√5 + 2√10

= 2(2.23) + 2(3.16)

= 10.78 units.

So, perimeter of the kite is 10.78 units.