FINDING AREA OF IRREGULAR SHAPES

Find the area of each of these shapes. The diagrams have not been drawn accurately.

Problem 1 :

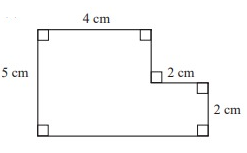
Solution :

By drawing a horizontal line, we can divide the given shape into two rectangles.

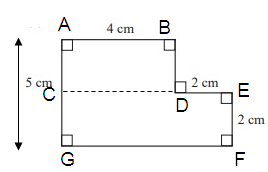
(1) ABCD is a rectangle

(2) CEFG is a rectangle

Area of the given polygon = Area of the rectangle ABCD + Area of the triangle DEFG

Area of the rectangle ABCD :

Length  AB = 4 cm, AG = 5 cm

AG = AC + CG

5 = AC + 2

AC = 3 cm

Width AC = 3 cm

= length × width

= 4 × 3

= 12 cm² --- (1)

Area of the triangle CEFG :

Length  CE = (4 + 2) ==> 6 cm

Width EF = 2 cm

= length × width

= 6 × 2

= 12 cm² --- (2)

Area of the given shape :

= (1) + (2)

= 12 + 12

 = 24 cm²

Problem 2 :

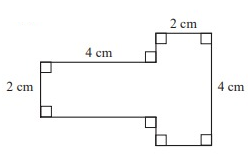
Solution :

By drawing a vertical line, we can divide the given shape into two rectangles.

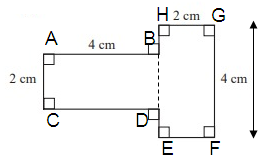
(1) ABCD is a rectangle

(2) EFHG is a rectangle

Area of the given polygon = Area of the rectangle ABCD + Area of the rectangle EFGH

Area of the rectangle ABCD :

Length  AB = 4 cm

Width AC = 2 cm

= length × width

= 4 × 2

= 8 cm² --- (1)

Area of the rectangle EFGH :

Length  HG = 2 cm

Width GF = 4 cm

= length × width

= 2 × 4

= 8 cm² --- (2)

Area of the given shape :

= (1) + (2)

= 8 + 8

 = 16 cm²

Problem 3 :

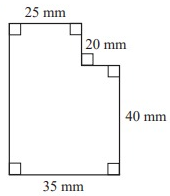
Solution :

By drawing a horizontal line, we can divide the given shape into two parts (rectangle and square) as shown below.

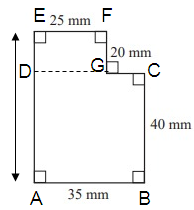
(1) ABCD is a square

(2) EFDG is a rectangle

Area of the given polygon = Area of the rectangle ABCD + Area of the triangle EFGD

Area of the rectangle ABCD :

Length  AB = 35 mm

Width BC = 40 mm

= length × width

= 35 × 40

= 1400 mm² --- (1)

Area of the triangle EFGD :

Length  HG = 25 mm

Width GF = 20 mm

= length × width

= 25 × 20

= 500 mm² --- (2)

Area of the given shape :

= (1) + (2)

= 1400 + 500

 = 1900 mm²

Problem 4 :

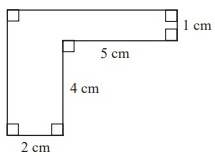
Solution :

By drawing a vertical line, we can divide the given shape into two rectangles.

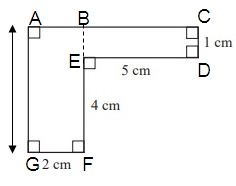
(1) ABGF is a rectangle

(2) BCDE is a rectangle

Area of the given polygon = Area of the rectangle ABGF + Area of the triangle BCDE

Area of the rectangle ABGF :

Length GF = 2 cm

Width BF = BE + EF

= 1 + 4 

BF = 5 cm²

= length × width

= 2 × 5

= 10 cm² --- (1)

Area of the triangle BCDE :

Length  ED = 5 cm

Width CD = 1 cm

= length × width

= 5 × 1

= 5 cm² --- (2)

Area of the given shape :

= (1) + (2)

= 10 + 5

 = 15 cm²

Problem 5 :

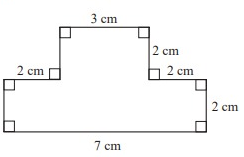
Solution :

By drawing a horizontal line, we can divide the given shape into two rectangles.

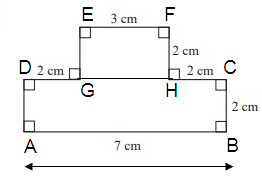
(1) ABCD is a rectangle

(2) EFHG is a rectangle

Area of the given polygon = Area of the rectangle ABCD + Area of the rectangle EFGH

Area of the rectangle ABCD :

Length  AB = 7 cm

Width CB = 2 cm

= length × width

= 7 × 2

= 14 cm² --- (1)

Area of the rectangle EFGH :

Length  EF = 3 cm

Width FH = 2 cm

= length × width

= 3 × 2

= 6 cm² --- (2)

Area of the given shape :

= (1) + (2)

= 14 + 6

 = 20 cm²

Problem 6 :

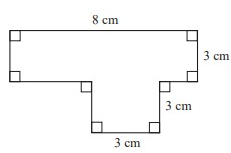
Solution :

By drawing a horizontal line, we can divide the given shape into two parts (rectangle and square) as shown below.

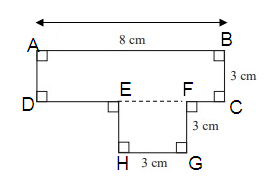
(1) ABCD is a rectangle

(2) EFGH is a square

Area of the given polygon = Area of the rectangle ABCD + Area of the square EFGH

Area of the rectangle ABCD :

Length  AB = 8 cm

Width BC = 3 cm

= length × width

= 8 × 3

= 24 cm² --- (1)

Area of the square EFGH :

= a²

= 3 × 3

= 9 cm² --- (2)

Area of the given shape :

= (1) + (2)

= 24 + 9

 = 33 cm²