FINDING ARC LENGTH OF A CIRCLE WORKSHEET

If s denotes the length of the arc of a circle of radius r subtended by a central angle θ, find the missing quantity.

Problem 1 :

s = 6.24 meters, θ = 2.6 radians, r =?

Solution

Problem 2 :

r = 2/3 feet, s = 14 feet, θ =?

Solution

Find the length s. Round the answer to three decimal places.

Problem 3 :

Solution

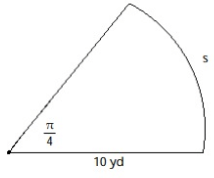
Problem 4 :

Solution

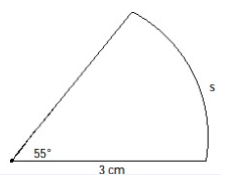
Problem 5 :

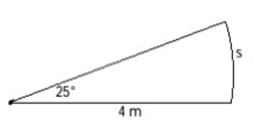
Problem 6 :

For a circle of radius 4 feet, find the arc length s subtended by central angle 60˚. Round to the nearest hundredth.

Solution

Problem 7 :

A pendulum swings though an angle of 30˚ each second. If the pendulum is 35 inches long. How far does its tip move each second? If necessary, round the answer to two decimal places.

Solution

Here s is the length of arc.

Problem 1 :

s = 12π/5 ; θ = π/2 ; r = ?

Solution

Problem 2 :

s = 50π/3 in ; θ = 5π/6 ; r = ?

Solution

Problem 3 :

s = 7ft ; θ = 3π/4 ; r = ?

Solution

Problem 4 :

s = 20 cm ; θ = 2π/3 ; r = ?

Solution

Problem 5 :

s = 12 in ; θ = 5 ; r = ?

Solution

Problem 6 :

s = 7 in ; θ = 3 ; r = ?

Solution

Problem 7 :

s = 15 m ; θ = 270 ; r = ?

Solution

Problem 8 :

s = 8 yd ; θ = 225 ; r = ?

Solution