FINDING ANGLE MEASURES OF A TRIANGLE USING RATIOS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
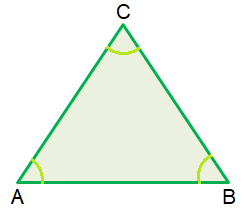
In the Above figure, ABC is a triangle.
The sum of the interior angles of a triangle is 180˚
<A + <B + <C = 180˚
Problem 1 :
The ratio of the angle measures of a triangle is 1: 1: 1. Find the angle measures. Then classify the triangle by its angle measures.
Solution :
Let the common ratio between the angles be x.
The sum of the interior angles of a triangle = 180˚
1x + 1x + 1x = 180˚
3x = 180˚
x = (180˚)/3
x = 60˚
The required angles are,
60˚ ; 1(60˚) = 60˚ ; 1(60˚) = 60˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
Problem 2 :
The ratio of the angle measures in a triangle is 6 : 5 : 4. Find the angle measures. Then classify the triangle by its angle measures.
Solution :
Let the common ratio between the angles be x.
The sum of interior angles of a triangle = 180˚
6x + 5x + 4x = 180˚
15x = 180˚
x = (180˚)/15
x = 12˚
The required angles are,
6(12˚) = 72˚ ; 5(12˚) = 60˚ ; 4(12˚) = 48˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
Find the value of x. Then classify the triangle by its angle measures.
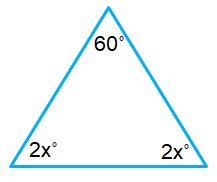
Problem 3 :
Solution :
The sum of the interior angles of a triangle = 180˚
60˚ + 2x˚ + 2x˚ = 180˚
60˚ + 4x˚ = 180˚
4x˚ = 180˚ – 60˚
4x˚ = 120˚
x˚ = (120˚)/4
x = 30˚
The required angles are,
60˚ ; 2(30˚) = 60˚ ; 2(30˚) = 60˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
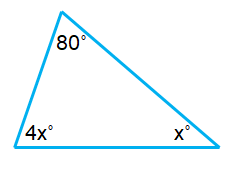
Problem 4 :
Solution :
The sum of the interior angles of a triangle = 180˚
80˚ + 4x˚ + x˚ = 180˚
80˚ + 5x˚ = 180˚
5x˚ = 180˚ – 80˚
5x˚ = 100˚
x = (100˚)/5
x = 20˚
The required angles are,
80˚ ; 4(20˚) = 80˚ ; 20˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
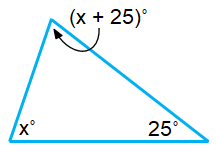
Problem 5 :
Solution :
The sum of the interior angles of a triangle = 180˚
x˚ + (x + 25)˚ + 25˚ = 1800˚
x˚ + x˚ + 25˚ + 25˚ = 180˚
2x˚ + 50˚ = 180˚
2x˚ = 180˚ – 50˚
2x˚ = 130˚
x = 65˚
The required angles are,
65˚ ; (65˚ + 25˚) ; 25˚
65˚ ; 90˚ ; 25˚
Since one of the angles is 90˚, it is a Right Angle Triangle.
Problem 6 :
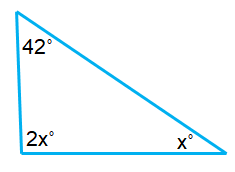
Solution :
42˚ + 2x˚ + x˚ = 180˚
42˚ + 3x˚ = 180˚
3x˚ = 180˚ – 42˚
3x˚ = 138˚
x = 46˚
The required angles are,
42˚ ; 2(46˚) = 92˚ ; 46˚
Since one of the angles is greater than 90˚, it is an Obtuse Angle Triangle.
Problem 7 :
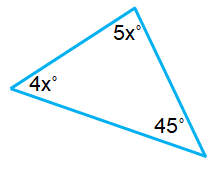
Solution :
4x˚ + 5x˚ + 45˚ = 180˚
60˚ + 4x˚ = 180˚
4x˚ = 180˚ – 60˚
4x˚ = 120˚
x = 30˚
The required angles are,
60˚ ; 2(30˚) = 60˚ ; 2(30˚) = 60˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
Problem 8 :
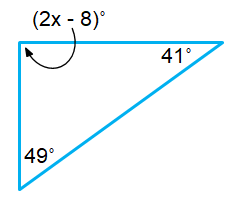
Solution :
The sum of the interior angles of a triangle = 180˚
49˚ + (2x – 8)˚ + 41˚ = 180˚
49˚ + 2x˚ - 8˚ + 41˚ = 180˚
82˚ + 2x˚ = 180˚
2x˚ = 180˚ – 82˚
x = (98˚)/2
x = 49˚
The required angles are,
49˚ ; (2(49)˚ - 8˚) ; 41˚
49˚ ; 90˚ ; 41˚
Since one of the angles is 90˚, it is a Right Angle Triangle.
Problem 9 :
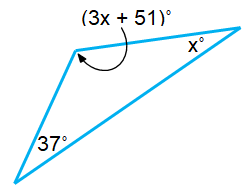
Solution :
(3x + 51)˚ + x˚ + 37˚ = 180˚
3x˚ + 51˚ + x˚ + 37˚ = 180˚
4x˚ + 51˚ +37˚ = 180˚
4x˚ + 88˚ = 180˚
4x˚ = 180˚ – 88˚
x˚ = 992˚)/4
x = 23˚
The required angles are,
(3(23)˚ + 51˚) ; 23˚ ; 37˚
120˚ ; 23˚ ; 37˚
Since one of the angles is greater than 90˚, it is an Obtuse Angle Triangle.
Problem 10 :
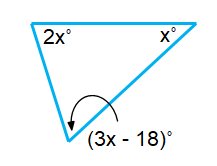
Solution :
2x˚ + x˚ +(3x – 18)˚ = 180˚
2x˚ + x˚ + 3x˚ – 18˚ = 180˚
3x˚ + 3x˚ - 18˚ = 180˚
6x˚ - 18˚ = 180˚
6x˚ = 180˚ + 18˚
x˚ = (198˚)/6
x = 33˚
The required angles are,
2(33˚) ; 33˚ + (3(33˚) – 18˚)
66˚ ; 33˚ ; 81˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
Problem 11 :
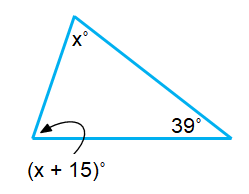
Solution :
(x + 15)˚ + x˚ + 39˚ = 180˚
(x˚ + 15˚) + x˚ + 39˚ = 180˚
2x˚ + 15˚ + 39˚ = 180˚
2x˚ + 54˚ = 180˚
2x˚ = 180˚ – 54˚
x˚ = (126˚)/2
x = 63˚
The required angles are,
(63˚ + 15˚) ; 63˚ ; 39˚
78˚ ; 63˚ ; 39˚
Since all the three angles are less than 90˚, it is an Acute Angle Triangle.
Problem 12 :
Find the value of x.
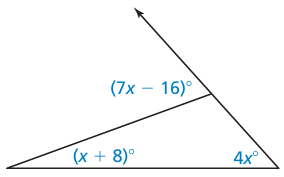
Solution :
Using exterior angle theorem,
x + 8 + 4x = 7x - 16
5x + 8 = 7x - 16
5x - 7x = -16 - 8
-2x = -24
x = 24/2
x = 12
So, the value of x is 12.
Problem 13 :
The ratio of the interior angle measures of a triangle is 2 : 3 : 5. What are the angle measures?
Solution :
The interior angles are 2x, 3x and 5x.
Sum of interior angles of triangle = 180
2x + 3x + 5x = 180
10x = 180
x = 180/10
x = 18
2x ==> 2(18) ==> 36
3x ==> 3(18) ==> 54
5x ==> 5(18) ==> 90
So, the required angles are 36, 54 and 90.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling