FINDING ANGLE MEASURES BETWEEN INTERSECTING LINES

Vertically opposite angles are angles that are opposite one another at a specific vertex and are created by two straight intersecting lines. Vertically opposite angles are equal to each other. These are sometimes called vertical angles.

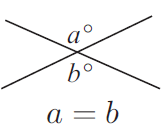
Proof :

∠COA + ∠AOD = 180 ----(1)

∠COB + ∠BOD = 180 ----(2)

(1) = (2)

∠COA + ∠AOD = ∠COB + ∠BOD

So, ∠COA = ∠BOD and  ∠COA = ∠BOD

Problem 1 :

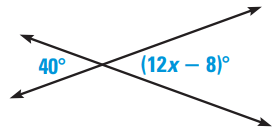
Solution :

Vertically opposite angles are equal.

40 = 12x - 8

Adding 8 on both sides

12x = 40 + 8

12x = 48

Divide by 12 on both sides.

x = 48/12

x = 4

Problem 2 :

Find the missing angles.

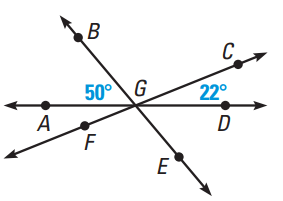
Solution :

∠AGB + ∠BGC + ∠CGD = 180

50 + ∠BGC + 22 = 180

72 + ∠BGC = 180

Subtracting 72, we get

∠BGC = 180 - 72

∠BGC = 108

∠FGE = 108

Vertically opposite angle are :

∠AGF = ∠CGD ==>  22

∠AGB = ∠EGD ==>  50

Problem 3 :

Solve for w.

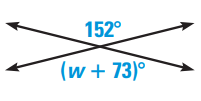
Solution :

152 and w + 73 are vertically opposite angles, they will be equal.

152 = w + 73

Subtracting 73 on both sides, we get

152 - 73 = w

w = 79

The value of w is 79.

Problem 4 :

Solve for n.

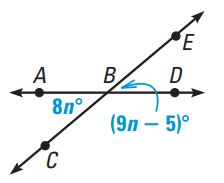
Solution :

∠ABC = ∠EBD (Vertically opposite angles)

8n = 9n - 5

Subtract 9n on both sides

8n - 9n = -5

-n = -5

So, n = 5

Problem 5 :

Solve for x.

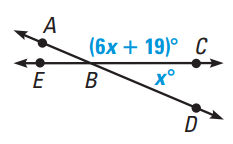
Solution :

∠ABC + ∠CBD = 180

6x + 19 + x = 180

7x + 19 = 180

Subtracting 19 on both sides.

7x = 180 - 19

7x = 161

Dividing by 7 on both sides.

x = 161/7

x = 23

Problem 6 :

Solve for p.

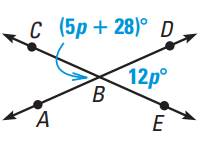
Solution :

∠ABC = ∠DBE (Vertically opposite angles)

5p + 28 = 12p

Subtracting 28, we get

5p = 12p - 28

Subtracting 12p on both sides.

5p - 12p = -28

-7p = -28

Divide by -7, we get

p = -28/(-7)

p = 4

Problem 7 :

Solve for x.

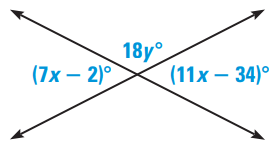
Solution :

Here 7x - 2 and 11x - 34 are vertically opposite angles.

7x - 2 and 18y are supplementary. So, they add upto 180.

7x - 2 = 11x - 34

Subtract 1x on both sides.

7x - 11x - 2 = -34

-4x - 2 = -34

Adding 2 on both sides,

-4x = -34 + 2

-4x = -32

Dividing by -4 on both sides.

x = -32/(-4)

x = 8

7x - 2 + 18y = 180

Applying the value of x, we get

7(8) - 2 + 18y = 180

56 - 2 + 18y = 180

54 + 18y = 180

Subtracting 54 on both sides.

18y = 180 - 54

18y = 126

Dividing by 18 on both sides.

y = 126/18

y = 7

Problem 8 :

Solve for x.

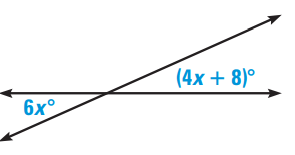
a. Use the Vertical Angles Theorem to write an equation.

b. Solve your equation to find the value of x.

c. Find the measures of the acute angles formed by the lines.

d. Find the measures of the obtuse angles formed by the lines.

Solution :

a) Here 6x and 4x + 8 are vertically angles.

6x = 4x + 8

b) Subtracting 4x on both sides.

6x - 4x = 8 

2x = 8

Dividing by 2, we get

x = 8/2

x = 4

c) Acute angle = 6x

= 6(4)

= 24

d) Let obtuse angle be "y"

24 + y = 180

Subtracting 24 on both sides.

y = 180 - 24

y = 156

Problem 9 :

The measures of two complementary angles have a ratio of 3:2. What is the measure of the larger angle?

Solution :

Since the given angles are complementary, the sum of these angles must be equal to 90.

From the given ratio, the required angles will be 3x and 2x.

3x + 2x = 90

5x = 90

x = 90/5

x = 18

3(18) ==> 54

2(18) ==> 36

So, the required angles are 36 and 54.

Problem 10 :

Write and solve a system of equations to fi nd the values of x and y

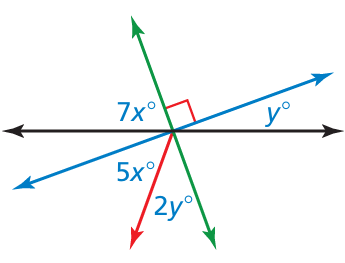
Solution :

Sum of angles in black line.

7x + 90 + y = 180

7x + y = 180 -  90

7x + y = 90 -------(1)

Sum of angles in green line.

7x + y + 5x + 2y = 180

12x + 3y = 180

4x + y = 60 -------(2)

(1) - (2)

7x + y - 4x - y = 90 - 60

3x = 30

x = 30/3

x = 10

Applying the value of x, we get

7(10) + y = 90

70 + y = 90

y = 90 - 70

y = 20

So, the values of x and y are 10 and 20 degree respectively.

Problem 11 :

Two angles form a linear pair. The measure of one angle is twice the measure of the other angle. Find the angles.

Solution :

Let x be the measure of other angle. Then the measure of first angle will be 2x.

Since they are linear pair, their sum will be 180 degree.

x + 2x = 180

3x = 180

x = 180/3

x = 60

2x = 2(60) ==> 120

So, the required angles are 60 and 120.