FINDING ABSOLUTE MAX AND MIN OF A FUNCTION WORKSHEET

Problem 1 :

The function g is given by

g(x) = 4x³ + 3x² - 6x + 1

what is the absolute minimum value of g on the closed interval [-2, 1] ?

A)  -7        B)  -3/4       C)  0        D)  2       E)  6

Solution

Problem 2 :

Find the absolute maximum and absolute minimum of the function under the given interval.

f(x) = 4x³ − 108x ; [0,5]

Solution

Problem 3 :

Find the absolute maximum and absolute minimum

Solution

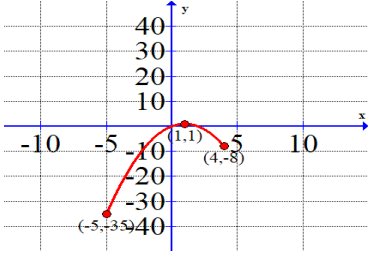
Problem 4 :

Find the absolute maximum and absolute minimum

Solution

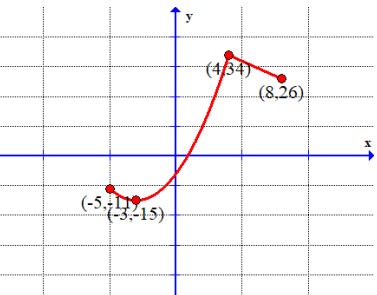
Problem 5 :

Let f be the function given by f(x) = x - 2 sin x for 0 ≤ x ≤ 2π

a) Find the intervals on which f is increasing and decreasing.

b) Find the absolute minimum and maximum value on the given interval.

Solution

For each problem, find all points of absolute minima and maxima on the given closed interval.

Problem 1 :

y = −x³ − 6x² − 9x + 3; [−3, −1]

Solution

Problem 2 :

Solution

Problem 3 :

f(x) = x³ + 6x² + 9 x + 3 ; [-4, 0]

Solution

Problem 4 :

f(x) = x⁴ - 3x²+ 4; [-1, 1]

Solution

Problem 5 :

Solution