FINDING LCM AND HCF USING PRIME FACTORIZATION WORKSHEET

Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the integers

Problem 1 :

26 and 91

Solution :

Decomposing the values 26 and 91 separately using prime factorization, we get

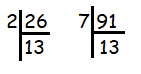
26 = 2 x 13

91 = 7 x 13

Common factor = 13

So, Highest common factor = 13.

Common multiples :

= 2 x 7 x 13

= 182

So, the least common multiple is 182.

Verifying the relationship :

LCM x HCF = Product of two numbers

13 x 182 = 26 x 91

2366 = 2366

Problem 2 :

510 and 92

Solution :

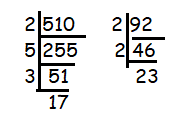
510 = 2 x 5 x 3 x 17

92 = 2 x 2 x 23

HCF = 2

LCM = 2² x 5 x 3 x 23 x 17

= 23460

Verifying the relationship :

LCM x HCF = Product of two numbers

2 x 23460 = 510 x 92

46920 = 46920

Problem 3 :

336 and 54

Solution :

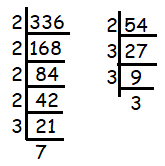
336 = 2 x 2 x 2 x 2 x 3 x 7 ==> 2⁴ x 3 x 7

54 = 2 x 3 x 3 x 3 ==> 2 x 3³

HCF = 2 x 3

= 6

LCM = 3³ x 2⁴ x 7

= 3024

Verifying the relationship :

LCM x HCF = Product of two numbers

6 x 3024 = 336 x 54

18144 = 18144

Find the HCF and LCM of the given numbers using prime factorization.

Problem 4 :

12, 15 and 21

Solution :

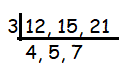
By multiplying the values outside, we get HCF.

HCF = 3

By multiplying all the values, we get LCM

LCM = 3 x 4 x 5 x 7

= 420

Problem 5 :

84, 90 and 120

Solution :

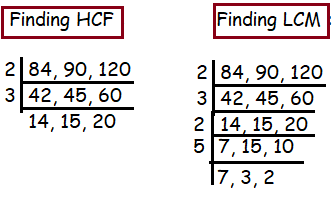
HCF = 2 x 3 ==> 6

LCM = 2³ x 3² x 5 x 7

= 2520

Problem 6 :

40, 36 and 126

Solution :

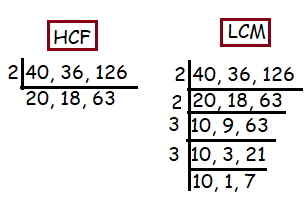
HCF = 2 

LCM = 2² x 3² x 10 x 7

= 2520

Problem 7 :

A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles.

Solution :

Length of courtyard = 18 m 72 cm

Converting the meter into cm, 1 m = 100 cm

18 m = 18 x 100 ==> 1800

18 m 72 cm = 1800 + 72 ==> 1872 cm

Width of courtyard = 13 m 20 cm

1 m = 100 cm

13 m = 1300 cm

13 m 20 cm = 1300 + 20 ==> 1320 cm

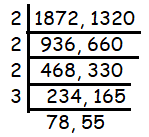
The measure should be common for both tiles.

= 24

Side length of square = 24

To figure out the number of tiles, we have to divide the total area by the area of square.

= (1872 x 1320) / 24²

= 4290

So, the total number of squares is 4290.

Problem 8 :

In a morning walk three persons step off together, their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that he can cover the distance in complete steps ?

Solution :

80 cm, 85 cm and 90 cm

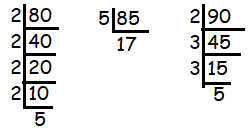
80 = 2⁴ x 5

85 = 5 x 17

90 = 2 x 3² x 5

Finding the least common multiple of these three measures, 

= 2⁴ x 3² x 5 x 17

= 12240

= 122 m 40 cm

So, the minimum distance can be covered by all three will be 122 m 40 cm.

Problem 9 :

A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60 and 72 km a day, round the field. When will they meet again ?

Solution :

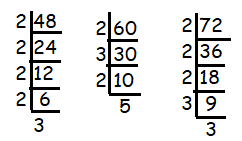
Number of miles covered by 1^st cyclist on each day

= 48, 96, 144,.......

Number of miles covered by 2^nd cyclist on each day

= 60, 120, 180, ............

Number of miles covered by 3^rd cyclist on each day

= 72, 144, 216, ...........

Number of days taken by 1^st cyclist to cover the ground

= 360/48

= 7.5 days

Number of days taken by 2^nd cyclist to cover the ground

= 360/60

= 6 days

Number of days taken by 3^rd cyclist to cover the ground

= 360/72

= 5 days

Least common multiple of 7.5, 6 and 5

75, 60 and 50

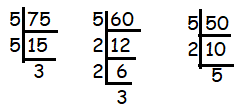
75 = 5² x 3

60 = 5 x 2² x 3

50 = 5² x 2

LCM = 5² x 2² x 3

= 300

Dividing by 10, we get

= 30 days

They all will meet again after 30 days.