FIND X AND Y INTERCEPTS OF ABSOLUTE VALUE FUNCTION

x-intercept :

The curve where it intersects the x-axis is known as x-intercept. To find x-intercept, we put y = 0.

y-intercept :

The curve where it intersects the y-axis is known as y-intercept. To find y-intercept, we put x = 0.

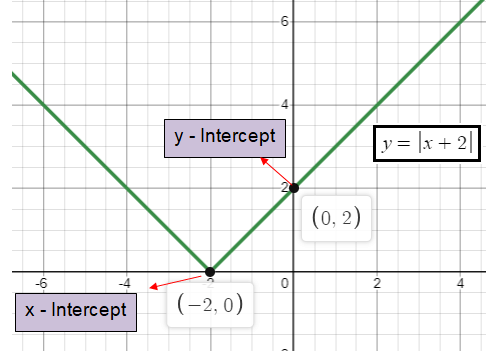
Find x and y intercepts for the absolute value function given below.

Problem 1 :

y = 3|x - 1| + 2

Solution :

x -Intercept:

put y = 0

3|x - 1| + 2 = 0

3|x - 1| = -2

|x - 1| = -2/3

This is not admissible. There is no real solution. So, there is no x-intercept. 

y -Intercept:

Put x = 0

y = 3|0 - 1| + 2

y = 3(1) + 2

y = 3 + 2

y = 5

y -Intercept is (0, 5).

Problem 2 :

y = 2|x|

Solution :

x -Intercept:

Put y = 0

2|x| = 0

x = 0

x -Intercept is (0, 0).  

y -Intercept:

Put x = 0

y = 2|0|

y = 0

y -Intercept is (0, 0).

Problem 3 :

y = |x| + 5

Solution :

x -Intercept :

Put y = 0

|x| + 5 = 0

|x| = - 5

The given function will not intersect the x-axis.

y -Intercept :

put x = 0

y = 0 + 5

y = 5

y -Intercept is (0, 5).

Problem 4 :

y = -2|x + 1| - 3

Solution :

x -Intercept:

Put y = 0

-2|x + 1| - 3 = 0

-2|x + 1| = 3

|x + 1| = -3/2

There is no x-intercept.

y -Intercept :

put x = 0

y = -2|0 + 1| - 3

= -2(1) - 3

= -2 - 3

y = -5

y -Intercept is (0, -5)   

Problem 5 :

y = -3/5|x + 3| + 10

Solution :

x -Intercept:

 put y = 0

-3/5|x + 3| + 10 = 0

-3/5|x + 3| = -10

3/5|x + 3| = 10

|x + 3| = 50/3

So, x-intercepts are (41/3, 0) and (-59/3, 0).

y -Intercept :

put x = 0

y = -3/5|0 + 3| + 10

y = -3/5(3) + 10

y = -9/5 + 10

y = (-9 + 50)/5

y = 41/5

y -Intercept is (0, 41/5)   

Problem 6 :

y = 15|x|

Solution :

x -Intercept :

put y = 0

15|x| = 0

x = 0

x -Intercept is (0, 0).

y -Intercept :

put x = 0

y = 15(0)

y = 0

y -Intercept is (0, 0).

Problem 7 :

y = 5/3|x + 2| - 1

Solution :

x -Intercept:

put y = 0

5/3|x + 2| - 1 = 0

5/3|x + 2| = 1

|x + 2| = 3/5

x -Intercept are (-7/5, 0) and (-13/5, 0).

y -Intercept :

put x = 0

y = 5/3|0 + 2| - 1

y = 5/3(2) - 1

y = 10/3 - 1

y = 7/3

y -Intercept (0, 7/3).

Problem 8 :

y = -2|x + 1| - 3

Solution :

x -Intercept :

put y = 0

-2|x + 1| - 3 = 0

-2|x + 1| = 3

|x + 1| = -3/2

There is no x-intercept.

y -Intercept :

put x = 0

y = -2|0 + 1| - 3

y = -2(1) - 3

y = -2 - 3

y = -5

y -Intercept is (0, -5).