FIND VERTICAL ASYMPTOTE AND END BEHAVIOR OF LOGARITHMIC
FUNCTION 

Vertical asymptote :

Vertical asymptote is the vertical line which is very closer to to the curve.

To find the vertical asymptote, we have to equate the argument to 0 and solve for x.

End behaviour of the logarithmic function :

Discussing the outputs when x approaches ∞ and -∞ is called end behaviour of the function.

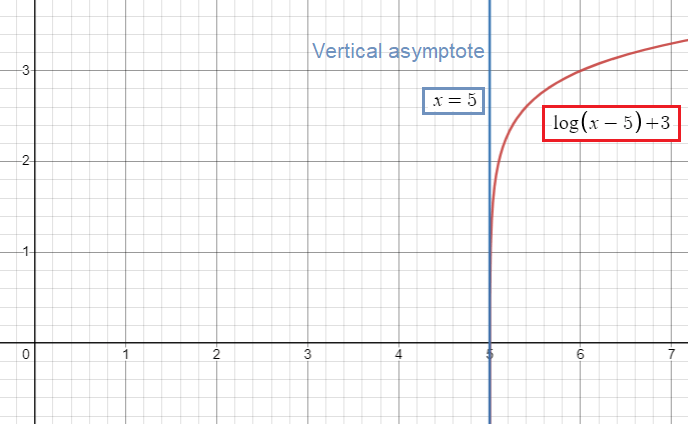
For the following exercise, state the domain, vertical asymptote, and end behaviour of the function.

Problem 1 :

f(x) = ln(2 - x)

Solution:

f(x) = ln(2 - x)

Domain:

2 - x > 0

-x > -2

x < 2

Domain: (-∞, 2)

Vertical asymptote:

2 - x = 0

-x = -2

x = 2

Vertical asymptote x = 2

End behaviour of function:

To identify end behaviour of the logarithmic function, let us have discussion about graph of the function.

f(x) = ln(2 - x)

f(x) = ln(-x + 2)

Since x is changed as -x, it should be reflection across y-axis and 2 units left horizontally.

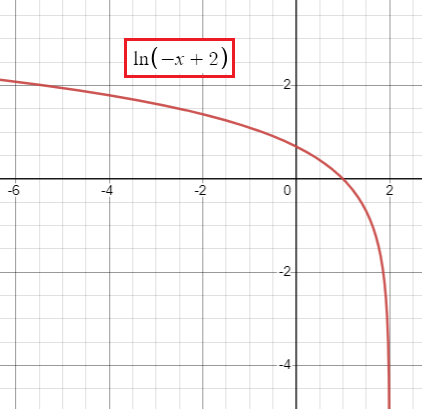
From the graph above,

lim _x->-∞ f(x) approaches ∞

and

lim _x->2 f(x) approaches -∞

Problem 2 :

f(x) = log(x - 3/7)

Solution:

f(x) = log(x - 3/7)

Domain:

x - 3/7 > 0

x > 3/7

Domain: (3/7, ∞)

Vertical asymptote:

x - 3/7 = 0

x = 3/7

vertical asymptote x = 3/7

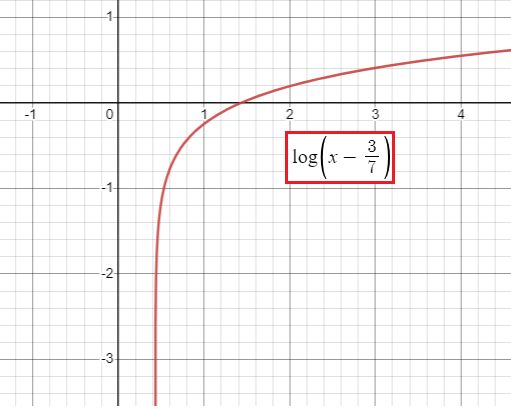
End behaviour of function:

To identify end behaviour of the logarithmic function, let us have discussion about graph of the function.

f(x) = log(x - 3/7)

No reflection, 3/7 units we have to move the graph to the right.

From the graph above,

lim _x->∞ f(x) approaches ∞

and

lim _x->3/7 f(x) approaches -∞

Problem 3 :

h(x) = -log(3x - 4) + 3

Solution:

h(x) = -log(3x - 4) + 3

Domain:

3x - 4 > 0

3x > 4

x > 4/3

Domain: (4/3, ∞)

Vertical asymptote:

3x - 4 = 0

3x = 4

x = 4/3

vertical asymptote x = 4/3

End behaviour of function:

To identify end behaviour of the logarithmic function, let us have discussion about graph of the function.

f(x) = -log(3x - 4) + 3

Reflection across x-axis, horizontal translation of 4/3 unit right and vertical translation of 3 units up.

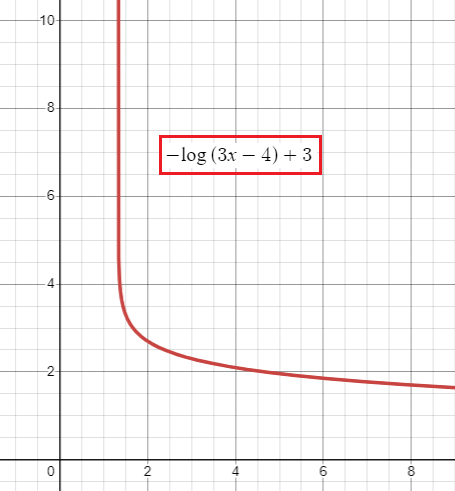
From the graph above,

lim _x->∞ f(x) approaches 0

and

lim _x->4/3 f(x) approaches ∞

Problem 4 :

g(x) = ln(2x + 6) - 5

Solution:

g(x) = ln(2x + 6) - 5

Domain:

2x + 6 > 0

2x > -6

x > -3

Domain: (-3, ∞)

Vertical asymptote:

2x + 6 = 0

2x = -6

x = -3

vertical asymptote x = -3

End behaviour of function:

f(x) =  ln(2x + 6) - 5

Reflection across x-axis, horizontal translation of 3 units left  and vertical translation of 5 units down.

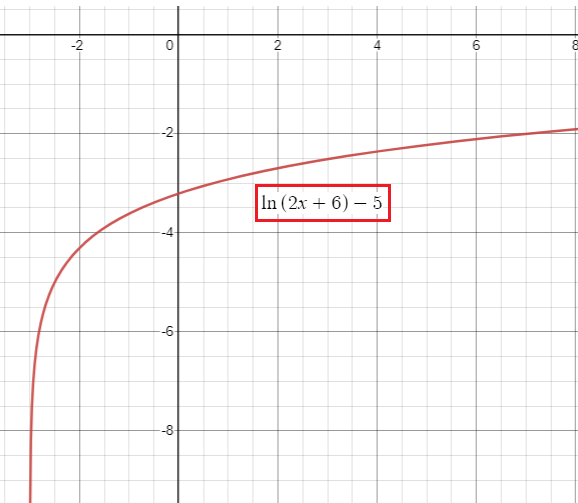
From the graph above,

lim _x->∞ f(x) approaches ∞

and

lim _x->-3 f(x) approaches -∞

Problem 5 :

f(x) = log₃(15 - 5x) + 6

Solution:

f(x) = log₃(15 - 5x) + 6

Domain:

15 - 5x > 0

15 > 5x

3 > x

x < 3

Domain: (-∞, 3)

Vertical asymptote:

15 - 5x = 0

15 = 5x

x = 3

vertical asymptote x = 3

End behaviour of function:

f(x) =  log₃(-5x + 15) + 6

or

f(x) =  log₃(-x + 3) + 6

Reflection across x-axis, horizontal translation of 3 units left  and vertical translation of 6 units up.

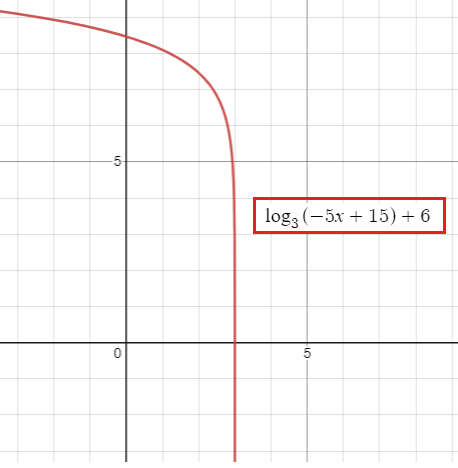
From the graph above,

lim _x->-∞ f(x) approaches ∞

and

lim _x->3 f(x) approaches -∞