FIND VERTEX AND AXIS OF SYMMETRY OF QUADRATIC FUNCTION THEN GRAPH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find the vertex form of the quadratic function from standard form y = ax2 + bx + c, we have to follow the steps given below.
(i) Take the coefficient of x2, from all the terms if there is.
(ii) Write the coefficient of x as a multiple of 2.
(iii) Get any one of the algebraic identities (a+b)2 or (a-b)2
Using shortcut
From the standard form of the equation, y = ax2 + bx + c
(i) Take the coefficient of x2, from all the terms if there is.
(ii) Take half of the coefficient of x and write it as (x - a)2 or (x + a)2. Here a is half the coefficient of x.
Axis of symmetry
Axis of symmetry is the vertical line that will divide the parabola into two equal parts.
Equation of axis of symmetry will be x = h.
Identify the vertex ans axis of symmetry of each by converting to vertex form. Then sketch the graph.
Problem 1 :
y = x2 - 12x + 36
Solution:
Vertex:
y = x2 - 12x + 36
y = x2 - 2(x)(6) + 62 - 62 + 36
y = (x - 6)2 - 36 + 36
y = (x - 6)2 + 0
By comparing this with the vertex form of parabola, we get
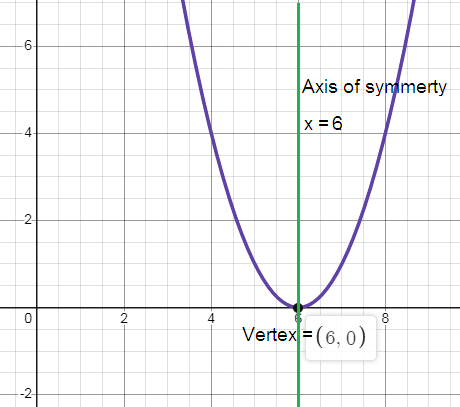
vertex (h, k) = (6, 0)
Axis of symmetry:
y = x2 - 12x + 36
a = 1, b = -12 and c = 36
Axis of symmetry x = 6.
Problem 2 :
y = -x2 - 6x - 10
Solution:
y = -x2 - 6x - 10
y = -(x2 + 6x + 10)
= -[(x2 + 2(x)(3) + 32 - 32 + 10)]
y = -[(x + 3)2 + 1]
y = -(x + 3)2 - 1
By comparing this with the vertex form of parabola, we get
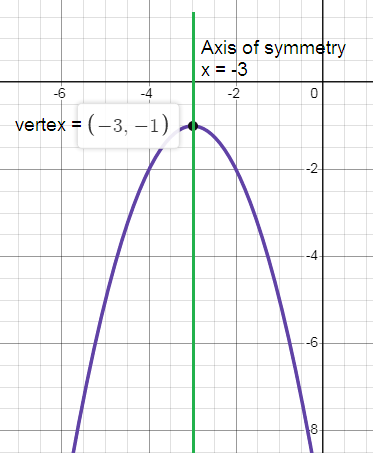
vertex (h, k) = (-3, -1)
Axis of symmetry:
y = -x2 - 6x - 10
y = -x2 - 6x - 10
a = -1, b = -6 and c = -10
Axis of symmetry x = -3.
Problem 3 :
y = x2 - 2x - 1
Solution:
y = x2 - 2x - 1
y = x2 - 2(x)(1) + 12 - 12 - 1
y = (x - 1)2 - 2
By comparing this with the vertex form of parabola, we get
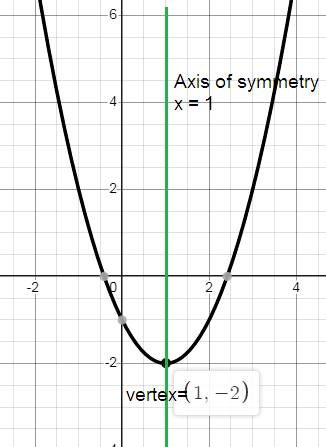
vertex (h, k) = (1, -2)
Axis of symmetry:
y = x2 - 2x - 1
a = 1, b = -2 and c = -1
Axis of symmetry x = 1.
Problem 4 :
y = -2x2 + 8x - 11
Solution:
y = -2x2 + 8x - 11
y = -2(x2 - 4x) - 11
= -2[x2 - 2(x)(2) + 22 - 22] - 11
= -2[(x - 2)2 - 4] - 11
= -2(x - 2)2 + 8 - 11
y = -2(x - 2)2 - 3
By comparing this with the vertex form of parabola, we get
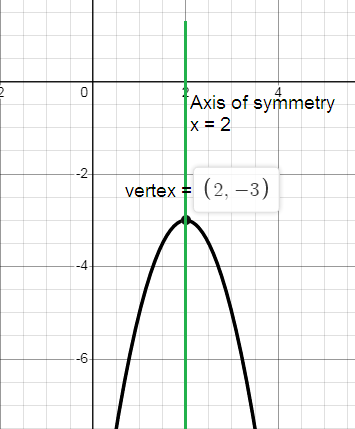
vertex (h, k) = (2, -3)
Axis of symmetry:
y = -2x2 + 8x - 11
a = -2, b = 8 and c = -11
Axis of symmetry x = 2.
Identify the vertex and axis of symmetry of each. Then sketch the graph.
Problem 5 :
f(x) = -3(x - 2)2 - 4
Solution:
Vertex:
f(x) = a(x - h)2 + k
f(x) = -3(x - 2)2 - 4
By comparing this with the vertex form of parabola, we get
(h, k) = (2, -4)
Axis of symmetry:
x = h
x = 2
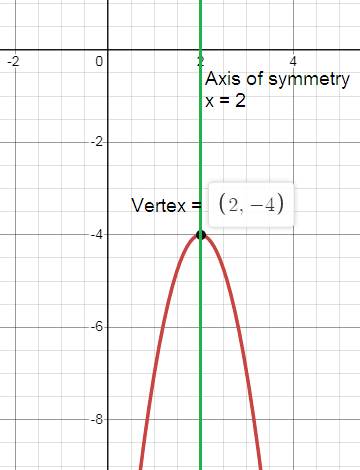
Problem 6 :
Solution:
Vertex:
f(x) = a(x - h)2 + k
By comparing this with the vertex form of parabola, we get
(h, k) = (1, 4)
Axis of symmetry:
x = h
x = 1
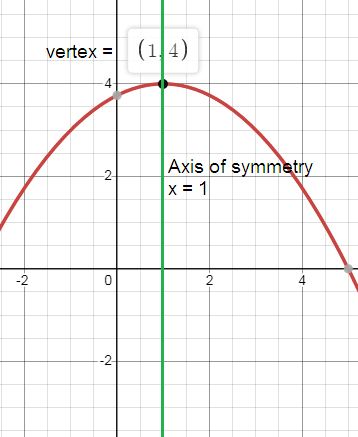
Problem 7 :
Solution:
Vertex:
f(x) = a(x - h)2 + k
By comparing this with the vertex form of parabola, we get
(h, k) = (-4, 3)
Axis of symmetry:
x = h
x = -4
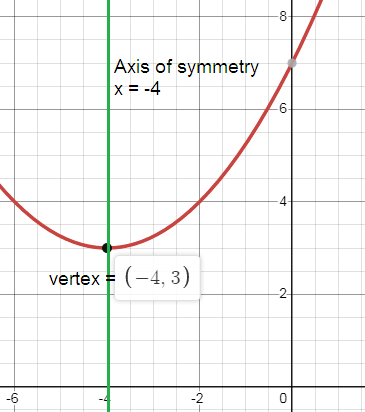
Problem 8 :
Solution:
Vertex:
f(x) = a(x - h)2 + k
By comparing this with the vertex form of parabola, we get
(h, k) = (-5, 2)
Axis of symmetry:
x = h
x = -5
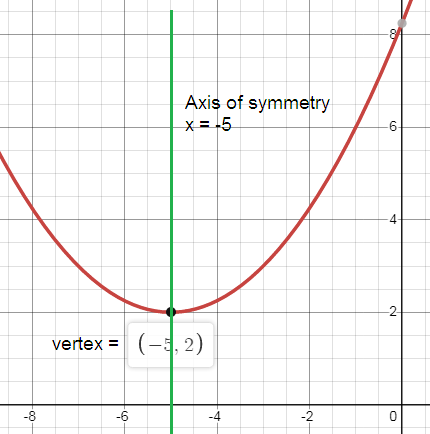
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling