FIND VERTEX AND AXIS OF SYMMETRY OF PARABOLA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is vertex ?
The graph of the quadratic function is called a parabola. The point where the graph turns is called the vertex.
If the graph opens upward, the y-coordinate of the vertex is the minimum and the graph is concave upwards.
If the graph opens downward, the y-coordinate of the vertex is the maximum and the graph is concave downwards.
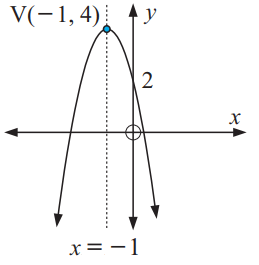
What is axis of symmetry ?
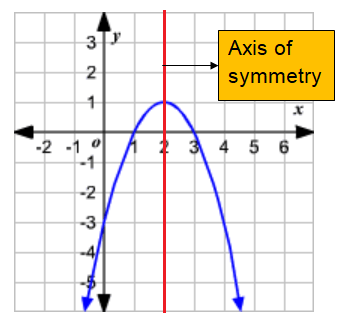
The axis of symmetry is the vertical line, which divides the parabola into two equal parts.
The axis of symmetry will always pass through the vertex of the parabola.
The quadratic function will be represented in three different forms.
- Factored form
- Vertex form and
- Standard form.
Here you can find examples of
How to find vertex and axis of symmetry from standard form ?
The quadratic function
y = ax2 + bx + c
x-coordinate of vertex can be found using the formula x = -b/2a and applying the value of x in the original function, we will receive value of y.
will have axis of symmetry at x = -b/2a
How to find vertex and axis of symmetry from vertex form ?
The quadratic function
y = a(x - h)2 + k
(h, k) is vertex and axis of symmetry at x = h
Use the vertex, axis of symmetry and y-intercept to graph:
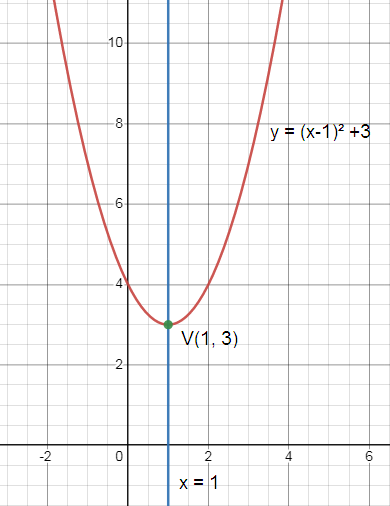
Problem 1 :
y = (x - 1)² + 3
Solution :
Comparing f(x) = a(x -
h)² + k and y = (x - 1)² + 3.
h = 1 and k = 3
Vertex of parabola :
(h, k) = (1, 3)
Axis of symmetry :
x = h = 1
x = 1
y- intercept :
x = 0
y = (0 - 1)² + 3
= (-1)² + 3
y = 4
y- Intercept = (0, 4)
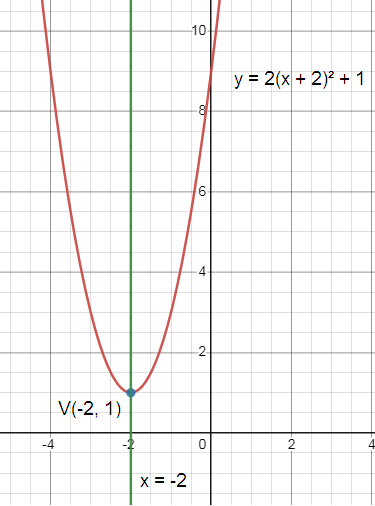
Problem 2 :
y = 2(x + 2)² + 1
Solution :
Comparing f(x) = a(x -
h)² + k and y = 2(x + 2)² + 1.
h = -2 and k = 1
Vertex of parabola :
(h, k) = (-2, 1)
Axis of symmetry:
x = h = -2
x = -2
y- intercept: x = 0
y = 2(0 + 2)² + 1
y = 8 + 1
y = 9
y- Intercept = (0, 9)
Problem 3 :
y = -2(x - 1)² - 3
Solution :
Comparing f(x) = a(x -
h)² + k and y = -2(x - 1)² - 3.
h = 1 and k = -3
Vertex of parabola :
(h, k) = (1, -3)
Axis of symmetry :
x = h = 1
x = 1
y- intercept :
x = 0
y = -2(0 - 1)² - 3
y = -5
y- Intercept = (0, -5)
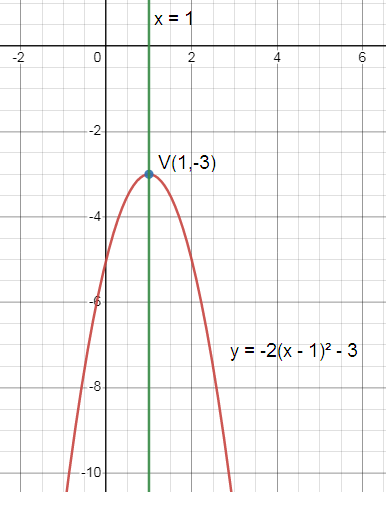
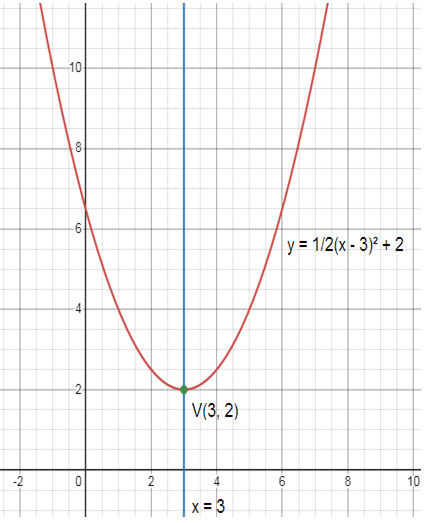
Problem 4 :
y = 1/2(x - 3)² + 2
Solution :
Comparing f(x) = a(x -
h)² + k and y = 1/2(x - 3)² + 2.
h = 3 and k = 2
Vertex of parabola :
(h, k) = (3, 2)
Axis of symmetry :
x = h = 3
x = 3
y- intercept :
x = 0
y = 1/2(0 - 3)² + 2
= 1/2(-3)² + 2
= 1/2 (9) + 2
y = 13/2
y- Intercept = (0, 13/2)
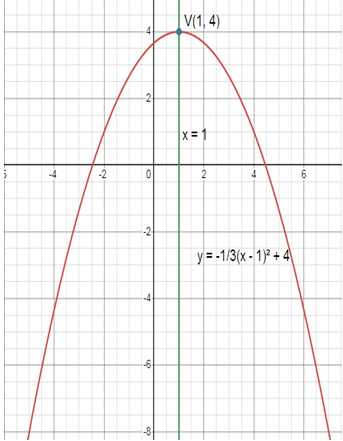
Problem 5 :
y = -1/3(x - 1)² + 4
Solution :
Comparing f(x) = a(x -
h)² + k and y = -1/3(x - 1)² + 4.
h = 1 and k = 4
Vertex of parabola :
(h, k) = (1, 4)
Axis of symmetry :
x = h = 1
x = 1
y- intercept :
Put x = 0
y = -1/3(0 - 1)² + 4
= -1/3 + 4
= 11/3
y = 3 2/3
y- Intercept = (0, 3 2/3)
Problem 6 :
y = -1/10 (x + 2)² - 3
Solution :
y = -1/10 (x + 2)² - 3
Comparing f(x) = a(x -
h)² + k and y = -1/10(x + 2)² - 3.
h = -2 and k = -3
Vertex of parabola :
(h, k) = (-2, -3)
Axis of symmetry :
x = h = -2
x = -2
y- intercept :
Put x = 0
y = -1/10 (0 + 2)² - 3
y = -1/10(4) - 3
y = -2/5 - 3
y = -17/5
y = -3 2/5
y- Intercept = (0, -3 2/5)
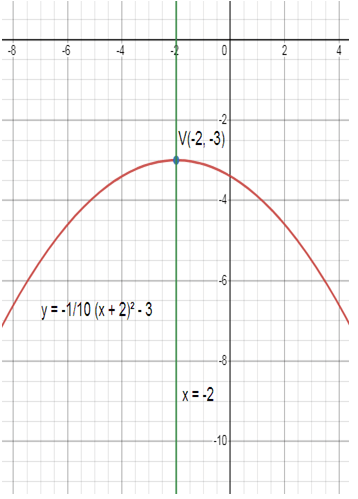
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling