FIND THE VOLUME OF PYRAMID

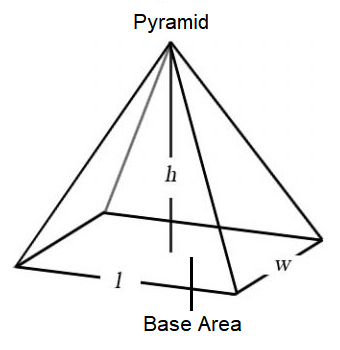
Volume of pyramid = (1/3) × Base area × Height

For rectangular pyramid,

Base Area = Length × Width

=  (1/3) × Length × Width × Height

For triangular pyramid,

Base Area = 1/2 × base × height

=  (1/3) × (1/2) × base × height × Height

Find the volume of the following Pyramid.

Problem 1 :

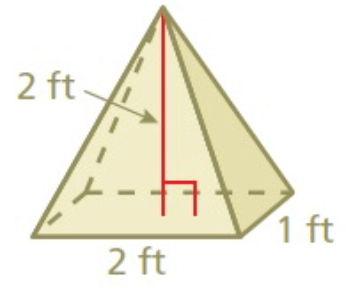
Solution :

Formula to find volume of pyramid is

= (1/3) × Base area × Height

Here Base Area is the rectangular shape.

So, Base Area =  length × width

= (1/3) ×  length × width × Height

We have,

Length = 2 ft, Width = 1 ft, and Height = 2 ft

= (1/3) × 1 × 2 × 2 

= 4/3

V = 1.33 ft³

Problem 2 :

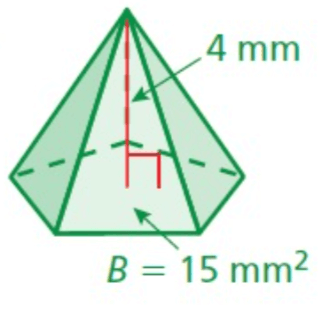
Solution :

Formula to find volume of pyramid is

= (1/3) × Base area × Height

Base area of the pyramid = 15mm²

Height of the pyramid = 4 mm.

Then, volume of the pyramid is

= (1/3) × 15 × 4

V = 20 mm³

Problem 3 :

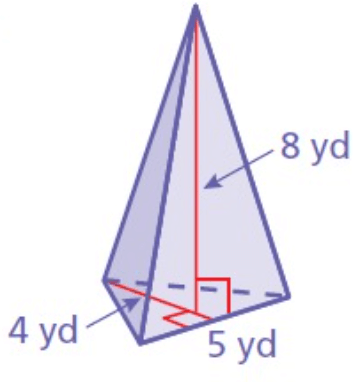
Solution :

Volume = (1/3) × Base area × Height

Here Base Area is the triangular shape.

So, Base Area =  1/2 × base × height

Here base = 5 yd, height (h₁) = 4 yd

= 1/2 × 5 × 4

= 10 yd²

We have,

Base Area = 10 yd² and Height = 8 yd

= (1/3) × 10 × 8

= (80)/3

V = 26.66 yd³

Problem 4 :

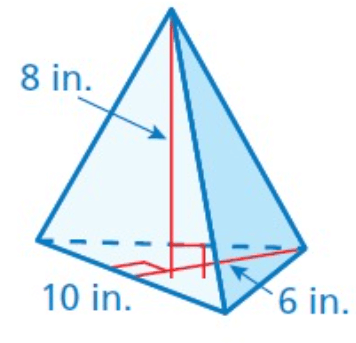
Solution :

Volume = (1/3) × Base area × Height

Here Base Area is the triangular shape.

So, Base Area =  1/2 × base × height

Here base = 10 in, height (h₁) = 6 in

= 1/2 × 10 × 6

= 30 in²

We have,

Base Area = 30 in² and Height (h₂)= 8 in

= (1/3) × 30 × 8

V = 80 in³

Problem 5 :

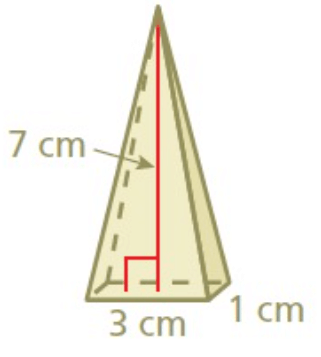
Solution :

Volume = (1/3) × Base area × Height

Here Base Area is the rectangular shape.

So, Base Area =  length × width

= (1/3) ×  length × width × Height

We have,

Length = 3 cm, Width = 1 cm, and Height = 7 cm

= (1/3) × 3 × 1 × 7

V = 7 cm³

Problem 6 :

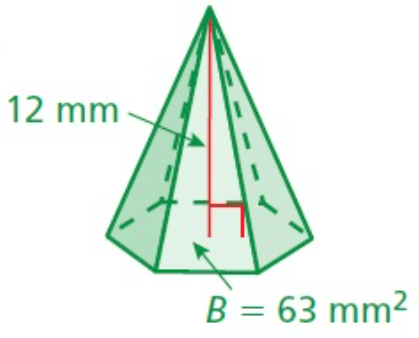
Solution:

Volume = (1/3) × Base area × Height

Base of the pyramid = 63mm²

Height of the pyramid = 12 mm.

= (1/3) × 63 × 12

V = 252 mm³

Problem 7 :

Do the two solids have the same volume? Explain.

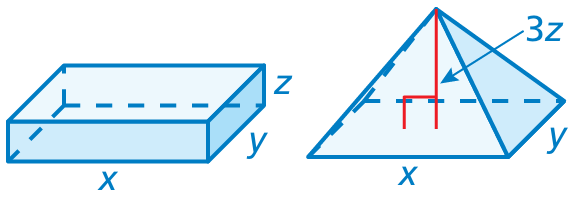
Solution :

Volume of prism = x⋅y⋅z

= xyz

Volume of pyramid = (1/3) ⋅ base area ⋅ height

= (1/3) ⋅ area of rectangle ⋅ height

= (1/3) ⋅ xy ⋅ (3z)

= xyz

Both solids are having the same volume.

Problem 8 :

A pyramid has a volume of 40 cubic feet and a height of 6 feet. Find one possible set of dimensions of the rectangular base.

Solution :

Volume of pyramid = 40 cubic feet

height = 6 feet

Base = rectangular in shape

Volume of pyramid = (1/3) x base area x height

40 = (1/3) x base area x 6

40 = 2 x base area

base area = 40/2

= 20 square feet

length = 10 ft, width = 2 ft (or) length = 4 ft and width = 5 ft

Problem 9 :

A recycle bin is in the shape of trapezoidial prism. The area of the base is 220 square inches and height is 24 inches. What is the volume of the recycle bin ?

Solution :

Area of the base = 220 square inches

Height = 24 inches

Volume of recycle bin = base area x height

= 220 x 24

= 5280 cubic inches

Problem 10 :

A water jug is in the shape of a prism. The area of the base is 100 square inches and the height is 20 inches. How many gallons of water will the water jug hold ?(1 gal = 231 in³)

Solution :

Area of  base = 100 square inches

height = 20 inches

Volume of water jug hold = 100 x 20

= 2000 cubic inches

1 gal = 231 cubic inches

Number of gallons of water = 2000/231

= 8.65 gallons

Problem 11 :

The sign made of solid wood is in the shape of triangle. The base is a triangle with the base of 6 feet and height of 4 feet. The height of the sign is 7 feet. The wood costs $3 per cubic foot. What is the cost of the sign ?

Solution :

base = 6 feet

height = 4 feet

Area of base = 1/2 x base x height

= (1/2) x 4 x 6

= 12 square feet

Height of sign = 7 feet

Volume of shape = 12 x 7

= 84 cubic feet

Cost = $3 per cubic feet

Cost of sign = 84 x 3

= $252

Problem 12 :

Two pyramids with square bases have the same volume. One pyramid has a height of 6 centimeter and area of the base is 36 square centimeters

a) What is the volume of pyramids ?

b) The base of the other pyramid has a side length of 3 centimeters. What is the height of this pyramid ?

Solution :

Height of the pyramid = 6 cm

area of base = 36 square cm

Volume of first pyramid = (1/3) x base area x height 

= (1/3) x 36 x 6

= 72 square cm

Side length of square base = 3 cm

Volume of first pyramid = volume of second pyramid

72 = (1/3) x 32 x height

(72 x 3)/32 = height

height = 6.75 cm

So, the height of the second pyramid is 6.75 cm.