FIND THE VALUE OF TRIGONOMETERIC FUNCTIONS IN THE GIVEN QUADRANT

Problem 1:

Find sin θ if cos θ = 2/3, 0 < θ < π/2

Solution:

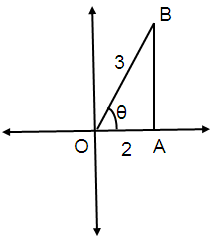
cos θ = Adjacent / Hypotenuse

Cos θ = 2/3

By using Pythagorean Theorem,

OB² = AB² + OA²

AB² = OB² - OA²

AB² = 3² - 2²

AB = √9 - 4

AB = √5

θ is in I quadrant.

All trigonometric values are positive.

sin θ = Opposite / Hypotenuse

sin θ = √5/3

Problem 2 :

Find cos θ, if sin θ = 2/5, π/2 < θ < π

Solution :

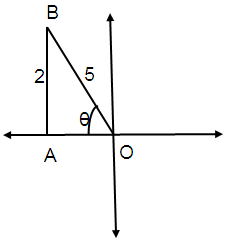
sin θ = Opposite / Hypotenuse

sin θ = 2/5

By using Pythagorean Theorem,

OB² = AB² + OA²

OA² = OB² - AB²

OA² = 5² - 2²

OA = √25 - 4

OA = √21

θ is in II quadrant.

In 2^nd quadrant only sin and cosec are positive.

cos θ = Adjacent / Hypotenuse

cos θ = -√21/5

Problem 3 :

Find cos θ if sin θ = -3/5, 3π/2 < θ < 2π

Solution :

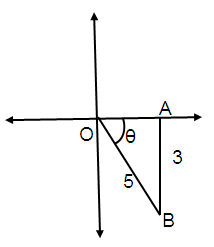
sin θ = Opposite / Hypotenuse

sin θ = -3/5

By using Pythagorean Theorem,

OB² = AB² + OA²

OA² = OB² - AB²

OA² = 5² - (-3)²

OA = √25 - 9

OA = √16

OA = 4

θ is in IV quadrant.

In 4^th quadrant only cos and sec are positive.

cos θ = Adjacent / Hypotenuse

cos θ = 4/5

Problem 4 :

Find sin θ if cos θ = -5/13, π < θ < 3π/2

Solution :

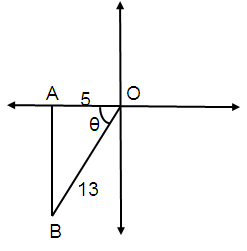
cos θ = Adjacent / Hypotenuse

Cos θ = -5/13

By using Pythagorean Theorem,

OB² = AB² + OA²

AB² = OB² - OA²

AB² = 13² - (-5)²

AB = √169 - 25

AB = √144

AB = 12

θ is in III quadrant.

In 3^rd quadrant only tan and cot are positive.

sin θ = Opposite / Hypotenuse

sin θ = -12/13

Problem 5 :

if sin x = 1/3 and π/2 < x < π, find tan x in radical (surd) form.

Solution : 

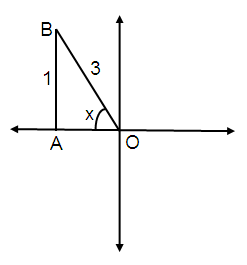
sin θ = Opposite / Hypotenuse

sin θ = 1/3

By using Pythagorean Theorem,

OB² = AB² + OA²

OA² = OB² - AB²

OA² = 3² - 1²

OA = √9 - 1

OA = √8

OA = 2√2

x is in II quadrant.

In 2^nd quadrant only sin and cosec are positive.

tan x = Opposite / Adjacent

tan x = -1/2√2

Problem 6 :

if cos x = 1/5 and 3π/2 < x < 2π, find tan x in radical (surd) form.

Solution :

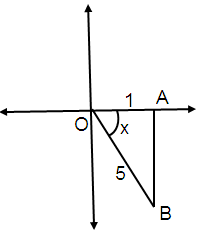
cos θ = Adjacent / Hypotenuse

cos θ = 1/5

By using Pythagorean Theorem,

OB² = AB² + OA²

AB² = OB² - OA²

AB² = 5² - 1²

AB = √25 - 1

AB = √24

AB = 2√6

x is in IV quadrant.

In 4^th quadrant only cos and sec are positive.

tan x = Opposite / Adjacent

tan x = -2√6 / 1

tan x = -2√6

Problem 7 :

if sin x = -1/√3 and π < x < 3π/2, find tan x in radical (surd) form.

Solution :

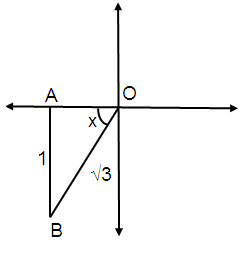
sin θ = Opposite / Hypotenuse

sin θ = -1/√3

By using Pythagorean Theorem,

OB² = AB² + OA²

OA² = OB² - AB²

OA² = (√3)² - 1²

OA = 3 - 1

OA = √2

x is in III quadrant.

In 3^rd quadrant only tan and cot are positive.

tan x = Opposite / Adjacent

tan x = 1/√2

Problem 8 :

if cos x = -3/4 and π/2 < x < π, find tan x in radical (surd) form.

Solution :

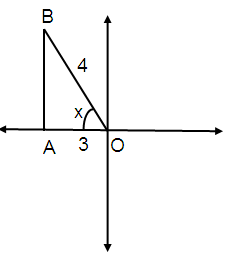
cos θ = Adjacent / Hypotenuse

cos θ = -3/4

By using Pythagorean Theorem,

OB² = AB² + OA²

AB² = OB² - OA²

AB² = 4² - 3²

AB = √16 - 9

AB = √7

x is in II quadrant.

In 2^nd quadrant only sin and cosec are positive.

tan x = Opposite / Adjacent

tan x = -√7/3

Problem 9 :

Find sin x and cos x given that:

tan x = 2/3 and 0 < x < π/2

Solution :

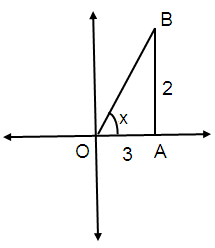
tan x = Opposite / Adjacent

tan x = 2/3

By using Pythagorean Theorem,

OB² = AB² + OA²

OB² = 2² + 3²

OB = √4 + 9

OB = √13

x is in I quadrant.

All trigonometric values are positive.

sin θ = Opposite / Hypotenuse

Sin θ = 2/√13

cos θ = Adjacent / Hypotenuse

cos θ = 3/√13

Problem 10 :

tan x = -4/3 and π/2 < x < π

Solution :

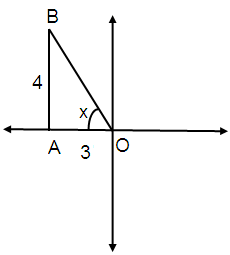
tan x = Opposite / Adjacent

tan x = -4/3

By using Pythagorean Theorem,

OB² = AB² + OA²

OB² = 4² + 3²

OB = √16 + 9

OB = √25

OB = 5

x is in II quadrant.

In 2^nd quadrant only sin and cosec are positive.

sin θ = Opposite / Hypotenuse

Sin θ = 4/5

cos θ = Adjacent / Hypotenuse

cos θ = -3/5

Problem 11 :

tan x = √5/3 and π < x < 3π/2

Solution :

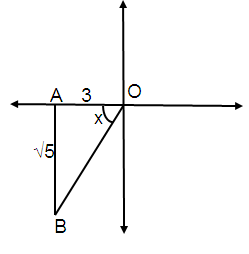
tan x = Opposite / Adjacent

tan x = √5/3

By using Pythagorean Theorem,

OB² = AB² + OA²

OB² = (√5)² + 3²

OB = √5 + 9

OB = √14

x is in III quadrant.

In 3^rd quadrant only tan and cot are positive.

sin θ = Opposite / Hypotenuse

sin θ = -√5/√14

cos θ = Adjacent / Hypotenuse

cos θ = -3/√14

Problem 12 :

tan x = -12/5 and 3π/2 < x < 2π

Solution :

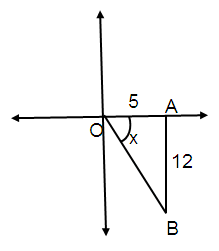
tan x = Opposite / Adjacent

tan x = -12/5

By using Pythagorean Theorem,

OB² = AB² + OA²

OB² = 12² + 5²

OB = 144 + 25

OB = √169

OB = 13

x is in IV quadrant.

In 4^th quadrant only cos and sec are positive.

sin θ = Opposite / Hypotenuse

sin θ = -12/13

cos θ = Adjacent / Hypotenuse

cos θ = 5/13