FIND THE VALUE OF THE DERIVATIVE AT EACH INDICATED EXTREMUM

Find the value of the derivative (if it exists) at each indicated extremum.

Problem 1 :

f(x) = x² / (x² + 4)

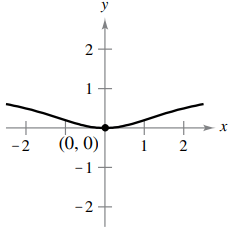
Solution :

f(x) = x² / (x² + 4)

Using quotient rule,

d(u/v) = (vu' - uv')/v²

f'(0) = 8(0)/(0² + 4)²

f'(0) = 0/16

f'(0) = 0

Problem 2 :

f(x) = cos (πx/2)

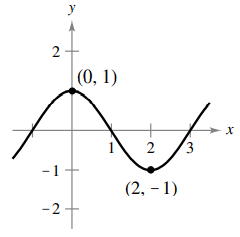
Solution :

f(x) = cos (πx/2)

f'(x) = - sin(πx/2) (π/2)

f'(0) = - sin(π(0)/2) (π/2) = sin 0 = 0

f'(2) = - sin(π(2)/2) (π/2) = -(π/2)(sin π) = 0

Problem 3 :

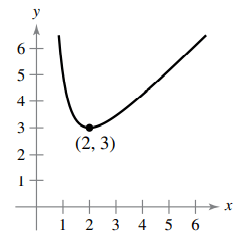
g(x) = x + (4/x²)

Solution :

g(x) = x + (4/x²)

g(x) = x + 4x^-2

g'(x) = 1 - (8/x³)

g'(2) = 1 - (8/2³)

= 1 - (8/8)

= 1 - 1

= 0

Problem 4 :

f(x) = -3x√(x + 1)

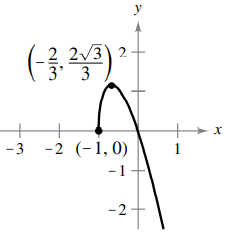
Solution :

Finding the derivative of f(x), using product rule.

Problem 5 :

f(x) = (x+ 2)^2/3

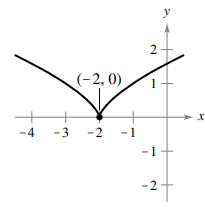
Solution :

f(x) = (x+ 2)^2/3

f'(x) = (2/3)(x + 2)^-1/3

At x = -2

f'(-2) = (2/3)(-2 + 2)^-1/3

f'(-2) = (2/3)[1/(0)^1/3]

f'(-2) = undefined

Problem 6 :

f(x) = 4 - |x|

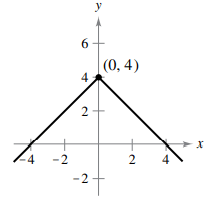
Solution :

f(x) = 4 - |x|

f'(x) = 0 - x/|x|

f'(x) = - x/|x|

So, the function is discontinuous.