FIND THE TURNING POINT OF A POLYNOMIAL FUNCTION

Graph each function. Identify the x-intercepts and the points where the local maximums and local minimums occur. Determine the intervals for which each function is increasing or decreasing.

Problem 1 :

f(x) = x³ − 3x² + 6

Solution :

Using graphing calculator 

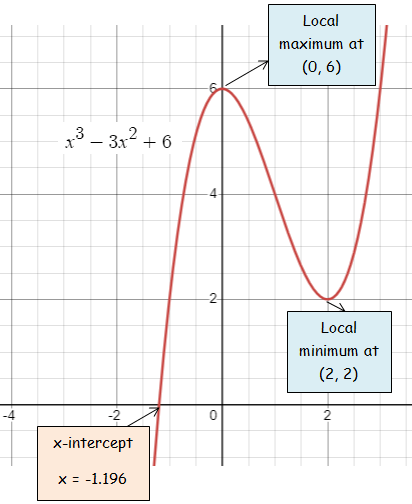
x - intercepts :

x-intercept at x = -1.196

Local minimum and maximum :

Local maximum at (0, 6) and local minimum at (2, 2).

Increasing and decreasing interval :

• When x < 0, f(x) is increasing.
• When x > 0 and x < 2, f(x) is decreasing.
• When x > 2, f(x) is increasing.

Increasing interval is (-∞, 0) and (2, ∞)

Decreasing interval is (0, 2).

Problem 2 :

g(x) = x⁴ − 6x³+ 3x² + 10x − 3

Solution :

Using graphing calculator 

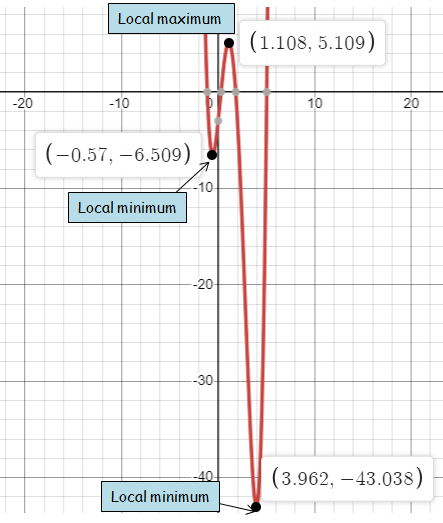
x-intercepts :

The function g(X) has four x-intercepts. x-intercept at

x = -1.137, 0.289, 1.186 and 5.033

Local minimum and maximum :

Local minimum is (-0.57, -6.509) and (-3.962, -43.038)

Local maximum is (1.108, 5.109)

Increasing and decreasing interval :

• g(x) is decreasing when x < -0.57 and 1.108< x < 3.962.
• g(x) is increasing when -0.57 < x < 1.108 and x > 3.962

Problem 3 :

Sketch a graph of a polynomial function f having the given characteristics.

• The graph of f has x-intercepts at x = −4, x = 0, and x = 2.

• f has a local maximum value when x= 1.

• f has a local minimum value when x=−2

Solution :

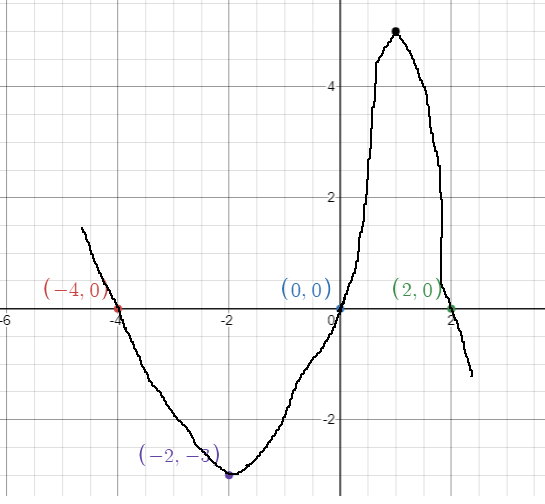
Problem 4 :

When a swimmer does the breaststroke, the function

S = −241t⁷+ 1060t⁶ − 1870t⁵+ 1650t⁴ − 737t³ + 144t²− 2.43t

models the speed S (in meters per second) of the swimmer during one complete stroke, where t is the number of seconds since the start of the stroke and 0 ≤ t ≤ 1.22. Use a graphing calculator to graph the function. At what time during the stroke is the swimmer traveling the fastest?

Solution :

Using the graphing calculator, by drawing the graph

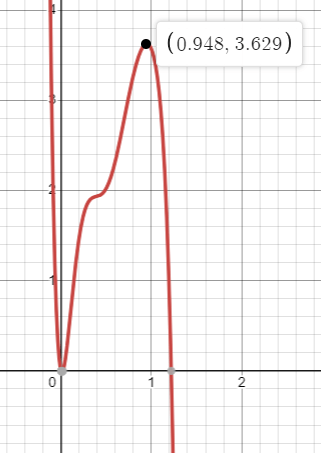
Local maximum appears at (0.948, 3.629). So, the swimmer is going fastest at 0.948 seconds and speed is 3.629 meter/second

Problem 5 :

A polynomial function of degree four is graphed as shown

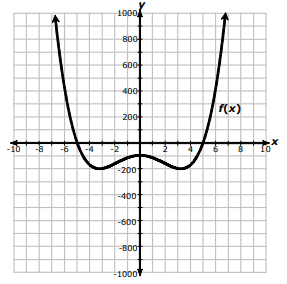
Based on this graph, which statement is true?

a) f(x) has a total of four roots and three local extrema.

b) f(x) has a total of two roots and three local extrema.

c) f(x) has a total of two roots and five extrema.

d) f(x) has a total of four roots and five extrema.

Solution :

From the given information, it is clear the graph has four roots. By analyzing key features, the polynomial function which has n roots, it will have (n -1) turning points.

Problem 6 :

Assuming that each is a comprehensive graph, answer each question

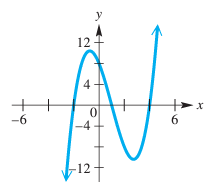
One of the following is an approximation for the local maximum point of the graph in A. Which one is it?

a) (0.73, 10.39)        b) (-0.73, 10.39)

c) (-0.73, -10.39)      d) (0.73, -10.39)

Solution :

By observing the graph, to the left of y-axis, there is local maximum.

To the left of origin, x-values are negative and maximum appears above the x-axis. So, option b is correct.