FIND THE REFERENCE ANGLE

Let A be an angle in standard position. The reference angle B associated with A is the acute angle formed by the terminal side of A and the x-axis.

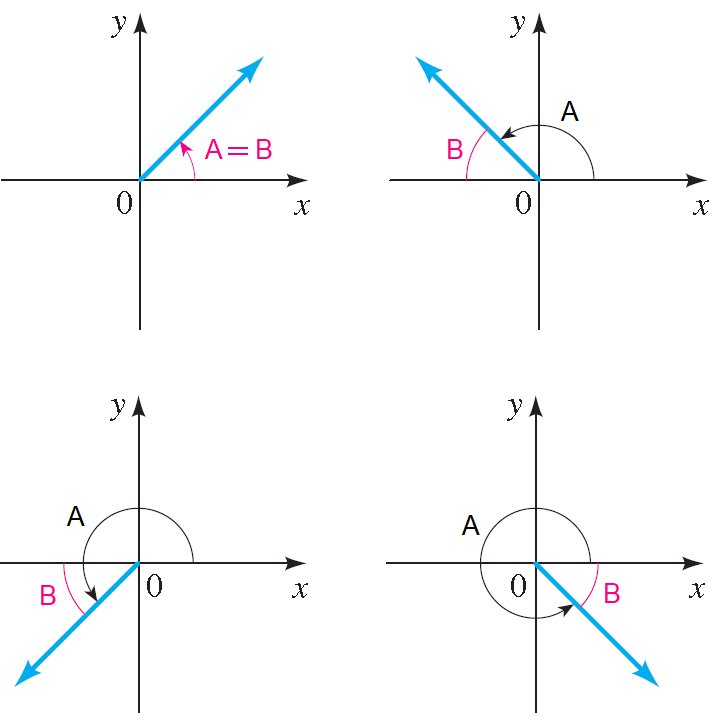
Ensure that the given angle is positive and it is between 0° and 360°.

What if the given angle does not meet the criteria above :

Let θ be the angle given.

Problem 1 :

325^º

Solution :

The given angle 325^º is positive and less than 360^º.

The angle 325^º  has its terminal side in quadrant IV. 

So, the reference angle is

= 360^º  - 325^º

= 35^º

Problem 2 :

-250^º

Solution :

The given angle -250^º is negative.

Add multiples of 360^º to -250^º to make the angle as positive such that it is between 0^º and 360^º.

-250^º + 360^º = 110^º

110^º is positive and less than 360^º.

The terminal side of the angle 110^º is in quadrant II.

So, the reference angle is

= 180^º  - 110^º

= 70^º

Problem 3 :

230^º

Solution :

The given angle 230^º is positive and less than 360^º.

The angle 230^º  has its terminal side in quadrant III. 

So, the reference angle is

= 230^º  - 180^º

= 50^º

Problem 4 :

335^º

Solution :

The given angle 335^º is positive and less than 360^º.

The angle 335^º  has its terminal side in quadrant IV. 

So, the reference angle is

= 360^º  - 335^º

= 25^º

Problem 5 :

-165^º

Solution :

The given angle -165^º is negative.

Add multiples of 360^º to -165^º to make the angle as positive such that it is between 0^º and 360^º.

-165^º + 360^º = 195^º

195^º is positive and less than 360^º.

The terminal side of the angle 195^º is in quadrant III.

So, the reference angle is

= 195^º  - 180^º

= 15^º

Problem 6 :

140^º

Solution :

The given angle 140^º is positive and less than 360^º.

The angle 140^º  has its terminal side in quadrant II. 

So, the reference angle is

= 180^º  - 140^º

= 40º

Problem 7 :

280^º

Solution :

The given angle 280^º is positive and less than 360^º.

The angle 280^º  has its terminal side in quadrant IV. 

So, the reference angle is

= 360^º  - 280^º

= 80^º

Problem 8 :

340^º

Solution :

The given angle 340^º is positive and less than 360^º.

The angle 340^º  has its terminal side in quadrant IV. 

So, the reference angle is

= 360^º  - 340^º

= 20^º

Problem 9 :

-120^º

Solution :

The given angle -120^º is negative.

Add multiples of 360^º to -120^º to make the angle as positive such that it is between 0^º and 360^º.

-120^º + 360^º = 240^º

240^º is positive and less than 360^º.

The terminal side of the angle 240^º is in quadrant III.

So, the reference angle is

= 240^º  - 180^º

= 60^º

Problem 10 :

-275^º

Solution :

The given angle -275^º is negative.

Add multiples of 360^º to -275^º to make the angle as positive such that it is between 0^º and 360^º.

-275^º + 360^º = 85^º

85^º is positive and less than 360^º.

The terminal side of the angle 85^º is in quadrant I.

So, the reference angle is

= 85^º