FIND THE POINT THAT DIVIDES THE LINE JOINING THE POINTS INTERNALLY

Problem 1 :

Find the coordinates of the point which divides the line segment joining the points A(4, -3) and B(9, 7) in the ration 3 : 2.

Solution:

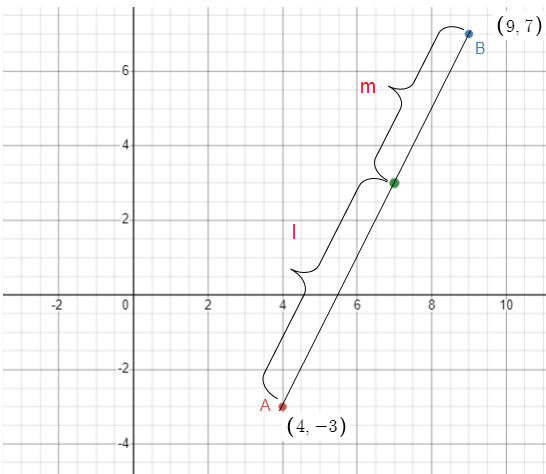
Let A(4, -3) and B(9, 7) be the given points.

Let the point P(x, y) divide the line AB internally in the ratio

3 : 2

By section formula,

Problem 2 :

Find the coordinates of the point which divides the line segment joining the points A(-1, 7) and B(4, -3) in the ration 2 : 3.

Solution:

Let A(-1, 7) and B(4, -3) be the given points.

Let the point P(x, y) divide the line AB internally in the ratio 2 : 3.

By section formula,

Problem 3 :

Find the coordinates of the point which divides the line segment joining the points A(-5, 11) and B(4, -7) in the ration 7 : 2.

Solution:

Let A(-5, 11) and B(4, -7) be the given points.

Let the point P(x, y) divide the line AB internally in the ratio 7 : 2.

By section formula,

Problem 4 :

If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.

Solution:

Given, a line segment joining the points A(-2, -2) and B(2, -4). P is a point on AB such that AP = 3/7 AB

Now, 

Therefore, point P divides AB internally in the ratio 3 : 4.

Hence, the coordinates of P are (-2/7, -20/7),

Problem 5 :

A(1, 1) and B(2, -3) are two points. If C is a point lying on the line segment AB such that CB = 2AC, find the coordinates of C.

Solution:

Using the section formula, if a point (x, y) divides the line joining the points (x₁, y₁) and (x₂, y₂) in the ratio l : m, then

Hence, the coordinates of C are (4/3, -1/2).

Problem 6 :

If A(1, 1) and B(-2, 3) are two points and C is a point on AB produced such that AC = 3AB, find the coordinates of C.

Solution:

Using the section formula, if a point (x, y) divides the line joining the points (x₁, y₁) and (x₂, y₂) externally in the ratio l : m, then (x, y) is 

Hence, the coordinates of  C are (-8, 7).