FIND THE POINT OF INTERSECTION OF THE LINES

Point of Intersection :

Point of intersection means the point at which two lines intersect.

These two lines are represented by the equation

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

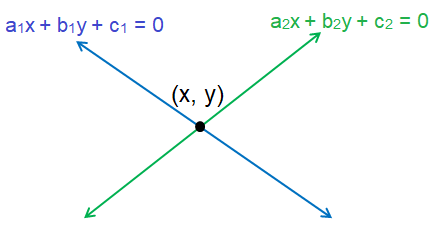
(x, y) is the point of intersection of the lines.

Problem 1 :

y = x + 4

5x – 3y = 0

Solution :

Given lines,

y - x = 4 -----(1)

5x – 3y = 0 -----(2)

(1) × (-3) ==> 3x - 3y = -12 ----(3)

Using Elimination Method :

Subtract (3) - (2), we get

3x - 3y - 5x + 3y = -12 - 0

-2x = -12

x = 6

By substituting x = 6 in (1), we get

y – 6 = 4

y = 4 + 6

y = 10

So, the point of intersection of the lines is (6, 10).

Problem 2 :

x + 2y = 8

y = 7 – 2x

Solution :

Given,

x + 2y = 8 -----(1)

2x + y = 7 -----(2)

(1) × 2 ==> 2x + 4y = 16 ----- (3)

Subtract (3) - (2), we get

2x + 4y - 2x - y = 16 - 7

3y = 9

y = 3

By substituting y = 3 in (1), we get

x + 2(3) = 8

x + 6 = 8

x = 8 – 6

x = 2

So, the point of intersection of the lines is (2, 3).

Problem 3 :

x – y = 5

2x + 3y = 4

Solution :

x – y = 5 ----- (1)

2x + 3y = 4 ----- (2)

(1) × 3 ==> 3x – 3y = 15 ----- (3)

Add (3) + (2), we get

3x - 3y + 2x + 3y = 15 + 4

5x = 19 

x = 19/5

x = 3.8

By substituting x = 19/5 in (1), we get

19/5 – y = 5

- y = 5 – 19/5

- y = (25 – 19) / 5

- y = 6/5

y = -6/5

y = -1.2

So, the point of intersection of the lines is (3.8, -1.2).

Problem 4 :

2x + y = 7

3x – 2y = 1

Solution :

2x + y = 7 ----- (1)

3x – 2y = 1----- (2)

(1) ∙ 2 ==> 4x + 2y = 14 ----- (3)

Add (3) + (2), we get

4x + 2y + 3x - 2y = 14 + 1

7x = 15

x = 15/7

x = 2.14

By substituting x = 15/7 in (1), we get

2(15/7) + y = 7

30/7 + y = 7

y = 7 – 30/7

y = (49 – 30) / 7

y = 19/7

y = 2.71

So, the point of intersection of the lines is (2.14, 2.71).

Problem 5 :

y = 3x – 1

x – y = 6

Solution :

-3x + y = -1 -----(1)

x – y = 6 -----(2)

Add (1) + (2), we get

-3x + y + x - y = -1 + 6

-2x = 5

x = -5/2

x = -2.5

By substituting x = -5/2 in (1), we get

-3(-5/2) + y = -1

15/2 + y = -1

y = -1 – 15/2

y = (-2-15) / 2

y = -17/2

y = -8.5

So, the point of intersection of the lines is (-2.5, -8.5).

Problem 6 :

y = -2x/3 + 2

2x + y = 6

Solution :

2x/3 + y = 2 ----- (1)

2x + y = 6 ----- (2)

Subtract (1) - (2), we get

2x/3 + y - 2x - y = 2 - 6

- 4x/3 = - 4

-4x = -12

x = 3

By substituting x = 3 in (1), we get

2(3/3) + y = 2

2 + y = 2

y = 2 – 2

y = 0

So, the point of  intersection of the lines is (3, 0).