FIND THE PERIMETER OF EACH TRIANGLE

The Formula for the Perimeter of a Triangle,

Perimeter = a + b + c

(where a, b, and c are the sides of a triangle)

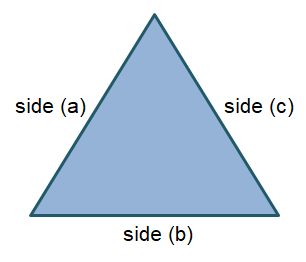
Problem 1 :

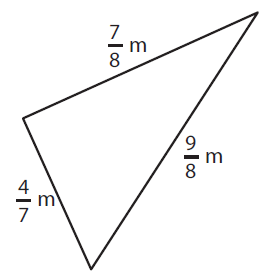
Solution :

Perimeter of triangle = a + b + c

Here, a = 4/7 m, b = 7/8 m and c = 9/8 m

= 4/7 m + 7/8 m + 9/8 m

= (4/7 + 7/8 + 9/8) m

LCM of 7, 8 and 8 is 56

= 32/56 + 49/56 + 63/56 m

= (144)/56 m

=18/7 m

Converting improper fraction into mixed fraction,

= 2  4/7 m

So, the perimeter of a triangle is 18/7 m or 2 4/7 m.

Problem 2 :

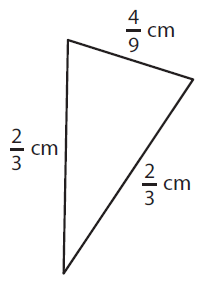
Solution :

Perimeter of triangle = a + b + c

Here a = 2/3 cm, b = 2/3 cm and c = 4/9 cm

= 2/3 cm + 2/3 cm + 4/9 cm

= (2/3 + 2/3 + 4/9) cm

LCM of 3, 3 and 9 is 9

= 6/9 + 6/9 + 4/9 cm

= 16/9 cm

Converting improper fraction into a mixed fraction,

= 1  7/9 cm

So, the perimeter of a triangle is 16/9 cm or 1 7/9 cm.

Problem 3 :

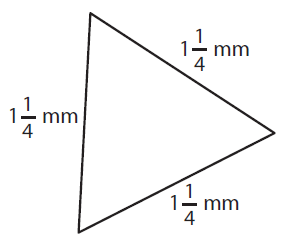
Solution :

Perimeter of triangle = a + b + c

Here a = 1 1/4 mm, b =1 1/4 mm and c =1 1/4 mm

=1 1/4 mm +1 1/4 mm +1 1/4 mm

= (5/4 + 5/4 + 5/4) mm

= 15/4 mm

= 3  3/4 mm

So, the perimeter of a triangle is 15/4 mm or 3 3/4 mm.

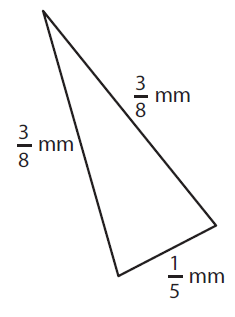
Problem 4 :

Solution :

Perimeter of triangle = a + b + c

Here a = 3/8 mm, b = 3/8 mm and c = 1/5 mm

= 3/8 mm + 3/8 mm + 1/5 mm

= (3/8 + 3/8 + 1/5) mm

LCM of 8, 8 and 5 is 40

= 15/40 + 15/40 + 8/40 mm

= 38/40 mm

= 19/20 mm

So, the perimeter of a triangle is 19/20 mm.

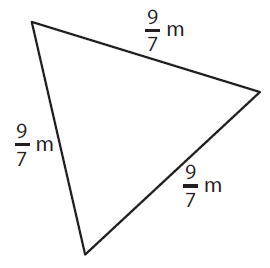
Problem 5 :

Solution :

Perimeter of triangle = a + b + c

Here a = 9/7 m, b = 9/7 m and c = 9/7 m

= 9/7 m + 9/7 m + 9/7 m

= (9/7 + 9/7 + 9/7) m

= 27/7 m

= 3  6/7 m

So, the perimeter of a triangle is 27/7 m or 3 6/7 m.

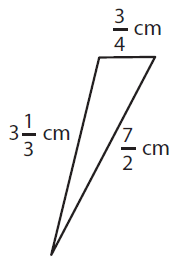
Problem 6 :

Solution :

Here a = 3 1/3 cm, b = 3/4 cm and c = 7/2 cm

= 3 1/3 cm + 3/4 cm + 7/2 cm

= (10/3 + 3/4 + 7/2) cm

LCM of 3, 4 and 2 is 12

= 40/12 + 9/12 + 42/12 cm

= 91/12 cm

= 7  7/12 cm

So, the perimeter of a triangle is 91/12 cm or 7 7/12 cm.

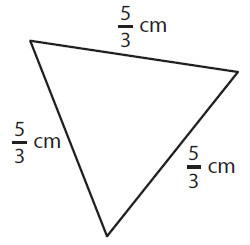
Problem 7 :

Solution :

Here a = 5/3 cm, b = 5/3 cm and c = 5/3 cm

= 5/3 cm + 5/3 cm + 5/3 cm

= (5/3 + 5/3 + 5/3) cm

= 15/3 cm

= 5 cm

So, the perimeter of a triangle is 5 cm. 

Problem 8 :

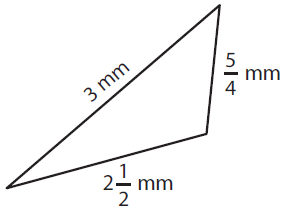
Solution :

Here a = 3 mm, b = 5/4 mm and c = 2 1/2 mm

= 3 mm + 5/4 mm + 2 1/2 mm

= (3 + 5/4 + 5/2) mm

= 3 + (5/4 + 5/2) 

= 3 + (15/4) 

= (12 + 15) / 4 

= 27/4 mm

= 6  3/4 mm

So, the perimeter of a triangle is 27/4 mm or 6  3/4 mm. 

Problem 9 :

The perimeter of a right angled triangle is 60 cm. Its hypotenuse is 26 cm. The area of the triangle is :

a)  120 cm²    b) 240 cm²       c)  390 cm²      d)  780 cm²

Solution :

Perimeter of any triangle will be the sum of sides.

Hypotenuse + sum of other two sides = 60 cm

26 + sum of other two sides = 60

Sum of the other two sides = 60 - 26

= 34

Since the given is right triangle, it should satisfy the Pythagorean theorem,

Let x be the base and 34 - x be the height

x² + (34 - x)² = 26² 

x² + 34² - 68x + x² = 26² 

2x² - 68x + 1156 - 676 = 0

2x² - 68x + 480 = 0

x² - 34x + 240 = 0

(x - 24)(x - 10) = 0

x = 24 and x = 10

When base = 24 cm and height = 10 cm

Area of triangle = (1/2) x 24 x 10

= 120 cm² 

Problem 10 :

The sides of a triangle are in the ratio of 1/2 : 1/3 : 1/4. If the perimeter is 52 cm, then the length of the smallest sides is 

a)  9 cm    b)  10 cm     d)  11 cm    d)  12 cm

Solution :

Side lengths of triangle are x/2, x/3 and x/4.

Perimeter = 52 cm

x/2 + x/3 + x/4 = 52

(6x + 4x + 3x)/12 = 52

13x / 12 = 52

x = 52(12/13)

x = 4(12)

x = 48 cm

x/2 = 48/2 ==> 24 cm

x/3 = 48/3 ==> 16 cm

x/4 = 48/4 ==> 12 cm

So, the smallest side of the triangle is 12 cm.

Problem 11 :

The perimeter of a triangle is 30 cm and its area is 30 cm². If the largest side measures 13 cm, then what is the length of the smallest side of the triangle ?

a)  3 cm     b)  4 cm     c)   5 cm     d)  6 cm

Solution :

From the information given above, we cannot decide what type of triangle it is. Let us consider it is a scalane triangle.

a, b and c are the sides of the triangle.

s = (a + b + c)/2

s = 30/2

s = 15

a = 13 cm, b and c = ?

13 + b + c = 30

b + c = 17

c = 17 - b

s - a = 15 - 13 ==> 2

√s (s - a)(s - b)(s - c) = 30

√15 x 2(15 - b)(15 - 17 + b) = 30

15 x 2(15 - b)(b - 2) = 900

(b - 2)(15 - b) = 900 / 30

15b - b² - 30 + 2b = 30

15b - b² + 2 b + 60 = 0

b² - 17 b + 60 = 0

(b - 12)(b - 5) = 0

b = 12 and b = 5

c = 17 - 12 ==> 5

So, the smallest side is 5 cm.