FIND THE MISSING MEASURES USING COSINE RULE

The cosine law can be used which is not a right triangle.

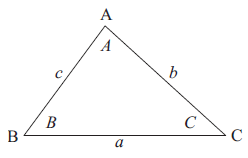
a² = b² + c² - 2bc cos A

b² = c² + a² - 2ac cos B

c² = a² + b² - 2ab cos C

Solve for the unknown in each triangle. Round to the nearest hundredth.

Problem 1 :

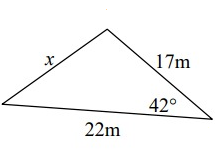
Solution:

a² = b² + c² - 2bc cos(A)

x² = 22² + 17² - 2(12)(17) cos 42°

x² = 484 + 289 - 748(0.74)

x² = 219.48

x = √219.48

x = 14.8 m

Problem 2 :

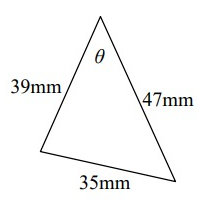
Solution:

Problem 3 :

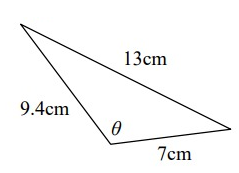
Solution:

Problem 4 :

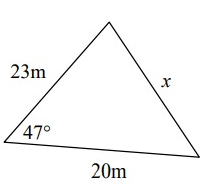
Solution:

a² = b² + c² - 2bc cos(A)

x² = 23² + 20² - 2(20)(23) cos 47°

x² = 529 + 400 - 920(0.68)

x² = 303.4

x = √303.4

x = 17.4 m

Problem 5 :

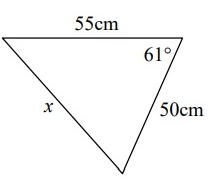
Solution:

a² = b² + c² - 2bc cos(A)

x² = 50² + 55² - 2(50)(55) cos 61°

x² = 2500 + 3025 - 5500(0.48)

x² = 2885

x = √2885

x = 53.46 cm

Problem 6 :

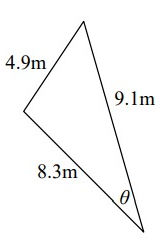
Solution: