FIND THE MISSING ANGLES OF THE TRIANGLE INSCRIBED A SEMI CIRCLE
Angle in a semicircle is right angle.
Find the
missing angles labelled in each of these circles
Problem 1 :
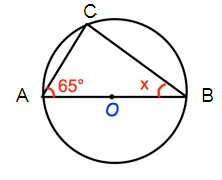
Solution :
∠CAB + ∠ACB + ∠CBA = 180º
65º + 90º + x = 180º
155º + x = 180º
x = 180º - 155º
x = 25º
So, the value of x is 25º.
Problem 2 :
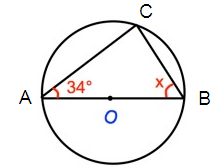
Solution :
∠CAB + ∠ACB + ∠CBA = 180º
34º + 90º + x = 180º
124º + x = 180º
x = 180º - 124º
x = 56º
So, the value of x is 56º.
Problem 3 :
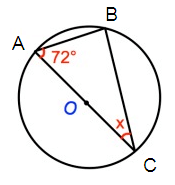
Solution :
∠ABC + ∠BCA + ∠CAB = 180º
90º + x + 72º = 180º
162º + x = 180º
x = 180º - 162º
x = 18º
So, the value of x is 18º.
Problem 4 :
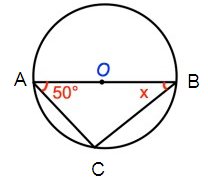
Solution :
∠ABC + ∠BCA + ∠CAB = 180º
x + 90º + 50º = 180º
x + 140º = 180º
x = 180º - 140º
x = 40º
So, the value of x is 40º.
Problem 5 :
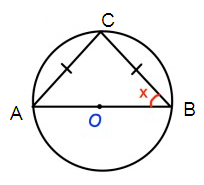
Let ∠ABC
∠ABC + ∠BCA + ∠CAB = 180º
x + 90º + x = 180º
2x + 90º = 180º
2x = 180º - 90
2x = 90º
Dividing 2 on both sides.
2x/2 = 90º/2
x = 45º
So, the value of x is 45º.
Problem 6 :
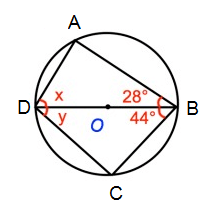
Solution :
∠ABD = 28º
∠BAD = 90º
∠ADB = x
∠ABD + ∠BAD + ∠ADB = 180º
28º + 90º + x = 180º
118º + x = 180º
x = 180º - 118º
x = 62º
∠BCD = 90º, ∠DBC = 44º, ∠BDC = y
∠BCD + ∠DBC + ∠BDC = 180º
90º + 44º + y = 180º
134º + y = 180º
y = 180º - 134º
y = 46º
So, the value of x and y is 62º and 46º.
Problem 7 :
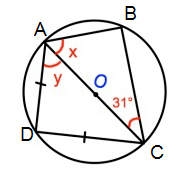
∠ABC = 90º
∠BCA = 31º
∠CAB = x
∠ABC + ∠BCA + ∠CAB = 180º
90º + 31º + x = 180º
121º + x = 180º
x = 180º - 121º
x = 59º
∠ACD = y, ∠CDA = 90º, ∠DAC = y
∠ACD + ∠CDA + ∠DAC = 180º
y + 90º + y = 180º
90º + 2y = 180º
2y = 180º - 90º
2y = 90º
Dividing 2 on both sides.
2y/2 = 90 º/2
y = 45º
So, the value of x and y is 59º and 45º.
Problem 8 :
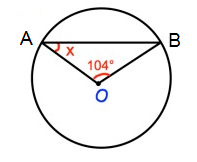
∠OAB + ∠ABO + ∠BOA = 180º
x + x + 104º = 180º
2x + 104º = 180º
2x = 180º - 104º
x = 76/2
x = 38
So, the value of x is 38º.
Problem 9 :
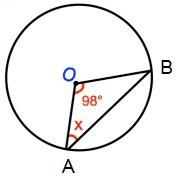
∠AOB + ∠OBA + ∠AOB = 180º
98º + x + x = 180º
2x = 180 - 98
2x = 82
x = 82/2
x = 41
Problem 10 :
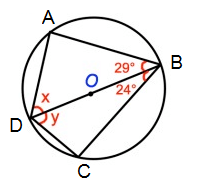
Solution :
∠ABD = 29º
∠BAD = 90º
∠ADB = x
∠ABD + ∠BAD + ∠ADB = 180º
29º + 90º + x = 180º
119º + x = 180º
x = 180º - 119º
x = 61º
∠BCD = 90º, ∠DBC = 24º, ∠BDC = y
∠BCD + ∠DBC + ∠BDC = 180º
90º + 24º + y = 180º
114º + y = 180º
y = 180º - 114º
y = 66º
So, the value of x and y is 61º and 66º.
Problem 11 :
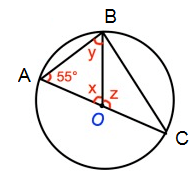
Solution :
∠OBA = y = 55º
∠OAB = 55º
∠ABO + ∠BOA + ∠OAB = 180º
55 + x + 55º = 180º
x + 110º = 180º
x = 180º - 110º
x = 70º
x and z are linear pair.
x + z = 180
70 + z = 180
z = 180 - 70
z = 110
Problem 12 :
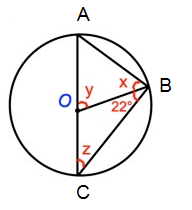
Solution :
x + 22 = 90
x = 90 - 22
x = 68
OB and OC are radii. If ∠OBC = 22, then ∠OCB = 22 = z.
y is exterior angle of triangle.
z + 22 = y
22 + 22 = y
44 = y
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling