FIND THE MISSING ANGLES IN CYCLIC QUADRILATERAL

A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral.

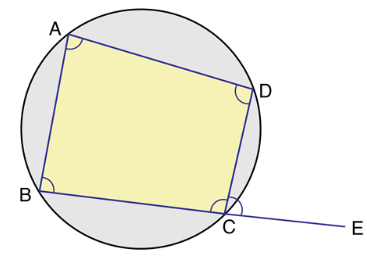
In which opposite angles are supplementary.

Exterior angle is equal to opposite interior angle. That is, in the above cyclic quadrilateral

∠DCE = ∠BAD

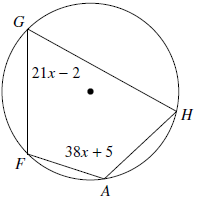
Problem 1 :

Find the value of x.

Solution :

Since the opposite angles are supplementary,

∠G + ∠A = 180

21x - 2 + 38x + 5 = 180

59x + 3 = 180

59x = 180 - 3

59x = 177

x = 177/59

x = 3

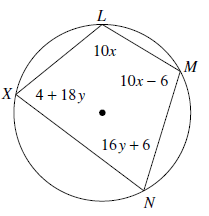
Problem 2 :

Solution :

∠L + ∠N = 180

10x + 16y + 6 = 180

10x + 16y = 180 - 6

10x + 16y = 174

Dividing by 2, we get

5x + 8y = 87  ------(1)

∠X + ∠M = 180

4 + 18y + 10x - 6 = 180

10x + 18y - 2 = 180

10x + 18y = 182

Dividing by 2, we get

5x + 9y = 91 ------(2)

(1) - (2)

(5x + 8y) - (5x + 9y) = 87 - 91

-y = -4

y = 4

By applying the value of y in (1), we get

5x + 8(4) = 87

5x + 32 = 87

5x = 87 - 32

5x = 55

x = 11

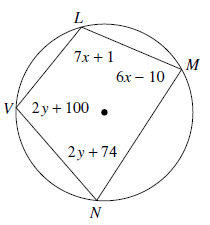
Problem 3 :

Solution :

7x + 1 + 2y + 74 = 180

7x + 2y + 75 = 180

7x + 2y = 180 - 75

7x + 2y = 105 ----(1)

2y + 100 + 6x - 10 = 180

2y + 6x + 90 = 180

6x + 2y = 90  ----(2)

(1) - (2)

7x - 6x = 105 - 90

x = 15

By applying the value of x in (1), we get

7(15) + 2y = 105

105 + 2y = 105

2y = 0

y = 0

Problem 4 :

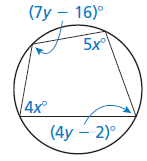
Solution :

Problem 5 :

Find ∠ABC, ∠AEC, ∠AGC, ∠ADC

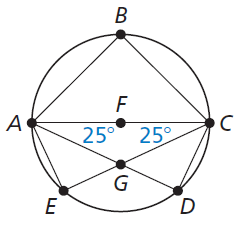
Solution :

In triangle ABC, ∠ABC = 90 (angle in a semicircle)

∠AEC = 90 and ∠ADC = 90

In triangle AGC,

∠AGC + ∠ACG + ∠CAG = 180

∠AGC + 25 + 25 = 180

∠AGC + 50 = 180

∠AGC = 180 - 50

∠AGC = 130

Problem 6 :

PQRS is a cyclic quadrilateral, and the side PS is extended to the point A. If ∠PQR = 80°, find ∠ASR

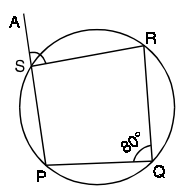
Solution :

∠PQR = ∠ASR = 80 (Exterior angle)

Problem 7 :

ABCD is a cyclic quadrilateral whose diagonals intersect at O. If ∠ACB = 50° and ∠ABC = 110°, find ∠BDC

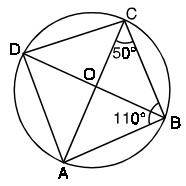
Solution :

∠ADC = 180 - ∠ABC

∠ADC = 180 - 110

∠ADC = 70

∠ADB = ∠ACB (Angle between the same arc AB)

∠ADB = ∠ACB (Angle between the same arc AB)

∠ADB = 50

∠ADC = ∠ADB + ∠BDC

70 = 50 + ∠BDC

∠BDC = 70 - 50

∠BDC = 20

Problem 8 :

In the given figure, ABCD is a cyclic quadrilateral whose diagonal intersect at P such that ∠DBC = 60^o and ∠BAC = 40^o. Find ∠BCD

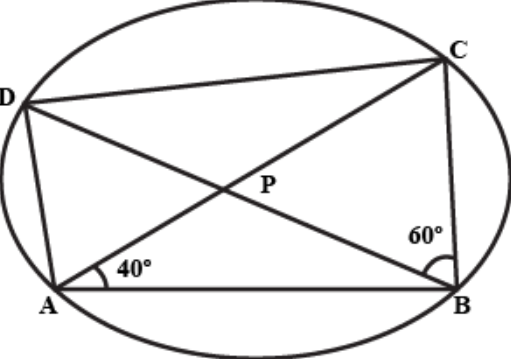
Solution :

∠DBC = ∠DAC (Angle between same arc DC)

∠DAC = 60

∠DAB = ∠DAC + ∠CAB

∠DAB = 60 + 40

∠DAB = 100

∠DCB = 180 - 100

∠DCB = 80