FIND THE MEAN OF THE GIVEN DATA

Problem 1 :

12.45, 12.99, 10.50, 11.25, 9.99, 12.72

Solution :

Mean = sum of all observations / number of observations

Here, n = 6

= (12.45 + 12.99 + 10.50 + 11.25 + 9.99 + 12.72) / 6

= (69.9) / 6

Mean = 11.65

Problem 2 :

28.8, 32.9, 32.5, 27.9, 30.4, 32.5, 31.6, 32.7

Solution :

Mean = sum of all observations / number of observations

Here, n = 8

= (28.8 + 32.9 + 32.5 + 27.9 + 30.4 + 32.5 + 31.6 + 32.7)

= (249.3) / 8

= 31.16

Problem 3 :

Four girls leaving a mall were asked how much money they had just spent. The amounts were $0, $14.95, $35.25, and $25.16. Find the mean amount of money spent.

Solution :

Mean = sum of all amount / number of girls

Here, n = 4

= (0 + 14.95 + 35.25 + 25.16) / 4

= 75.36 / 4

Mean = 18.84

She spent the money on average is $18.84.

Problem 4 :

Juan bought 5 shirts to wear to his new job. The costs of the shirts were $32.95, $38.50, $30.00, $17.45, and $24.25. Find the mean cost.

Solution :

Mean = sum of all shirt cost / number of shirts

Here, n = 5

= (32.95 + 38.50 + 30.00 + 17.45 + 24.25) / 5

= (143.15) / 5

= 28.63

The average cost is $28.63.

Problem 5 :

The number of minutes it took Jim to ride his bike to school for each of the past six days was 21, 18, 16, 19, 24 and 19. Find the mean number of minutes.

Solution :

Mean = sum of all days / total no of days

Here, n = 6

= (21 + 18 + 16 + 19 + 24 + 19) / 6

= (117)/6

= 19.5

The average number of minutes is 19.5.

Problem 6 :

Norris bought six books for his classes this semester. The costs of the books were $74.28, $120.95, $52.40, $10.59, $35.89, and $59.24. Find the mean cost.

Solution:

Mean = sum of all book cost / number of books

Here, n = 6

= (74.28 +120.95 + 52.40 + 10.59 + 35.89 + 59.24) / 6

=353.35 / 6

= 58.89

The average cost is $58.89.

Problem 7 :

The top eight hitters in a softball league have batting averages of .373, .360, .321, 321, .320, .312, .311, and .311. Find the mean of the batting averages. Round your answer to the nearest thousandth.

Solution :

Mean = sum of all batting averages / number of averages

Here, n = 8

= (.373 + .360 + .321, 321 + .320 + .312 + .311 + .311) / 8

= 2.629 / 8

= 0.328

The average of the batting  is 0.338.

Problem 8 :

The monthly snowfall at a ski resort over a six-month period was 60.3, 79.7, 50.9, 28.0, 47.4, and 46.1 inches. Find the mean snowfall.

Solution :

Mean = sum of all period / number inches

Here, n = 6

= (60.3 + 79.7 + 50.9 + 28.0 + 47.4 + 46.1) / 6

= 312.4 / 6

= 52.06

The average of snowfall is 52.06 inches.

Problem 9 :

An amusement park hires students for the summer. The students’ hourly wages are given in the table. Find the mean, median, and mode of the hourly wages.

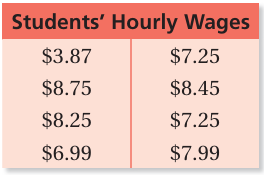
Solution :

Mean :

Arranging the wages from least to greatest,

3.87, 6.99, 7.25, 7.25, 7.99, 8.25, 8.45, 8.75

Number of students = 8

= (3.87 + 6.99 + 7.25 + 7.25 + 7.99 + 8.25 + 8.45 + 8.75) / 8

= 58.8/8

Mean = 7.35

Median :

3.87, 6.99, 7.25, 7.25, 7.99, 8.25, 8.45, 8.75

Median = (7.25 + 7.99)/2

= 15.64/2

= 7.62

So, the median is 7.62.

Mode :

7.25 is repeating more times. Then mode is $7.25.

Problem 10 :

In an English class, four students wrote essays of 1327, 1295, 1198 and 1456 words in length, respectively. What is the average length of these four essays?

Solution :

Average length = (1327 + 1295 + 1198 + 1456)/4

= 5276/4

= 1319

So, the average length of these four essays is 1319.

Problem 11 :

The average of eight numbers is 22. If we remove one number, the average of the remaining numbers is 19. What number was removed?

Solution :

Average of eight numbers = 22

After removing 1 number, average of seven numbers = 19

Sum of seven numbers / 7 = 19

Sum of seven numbers = 19(7)

= 133

Let x be the number which is removing.

(Sum of seven numbers + x)/8 = 22

(133 + x)/8 = 22

133 + x = 22(8)

133 + x = 176

x = 176 - 133

x = 43

So, the number which is removed is 43.

Problem 12 :

The teacher sets a goal for a class average of 92 on a test. Out of a class of 12 students, seven students scored 89 and four students scored 84. What must the remaining score be in order to reach the goal? Can it be done?

Solution :

Let x be the unknown.

Average = 92

Total number of students = 12

(7(89) + 4(84) + x)/12 = 92

623 + 336 + x = 92(12)

959 + x = 1104

x = 1104 - 959

x = 145

So, the remaining score is 145.