FIND MEAN MEDIAN AND MODE FROM A STEM AND LEAF PLOT

Problem 1 :

Find the data displayed in stem and leaf plot, find the

(i) Mean    (ii) Median and  (iii)  Mode

Solution :

The data values from the stem and leaf.

38, 39, 42, 42, 45, 50, 51, 51, 57, 59, 61, 63, 64, 70

Total number of data values = 14

i) Mean :

Mean = Sum of the value / Total number of values

= (38+39+42+42+45+50+51+51+57+59+61+63+64+70)/14

= 732/14

= 52.28

ii)  Median :

Number of quantities = 14

Median = [(14/2)^th value + ((14/2) + 1)^th value]/2

= (7^th value + 8^th value)/2

= (51 + 51)/2

= 51

iii)  Mode :

42 and 51 are modes.

Problem 2 :

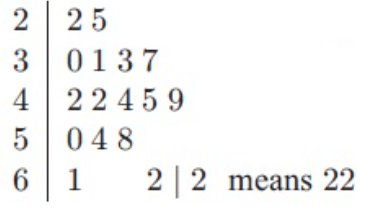
Find the data displayed in stem and leaf plot, find the

(i) Mean    (ii) Median and  (iii)  Mode

Solution :

22, 25, 30, 31, 33, 37, 42, 42, 44, 45, 49, 50, 54, 58, 61

i) Mean :

 (22+25+30+31+33+37+42+42+44+45+49+50+54+58+61)/15

= 623/15

= 41.53

ii) Median :

= (15 + 1)/2 ^th value

= 16/2 ^th value

= 8 ^th value

= 42

iii) Mode :

Most repeated term is 42

So, mode is 42.

Problem 3 :

Find the data displayed in stem and leaf plot, find the

(i) Mean    (ii) Median and  (iii)  Mode

Solution :

40, 46, 51, 52, 53, 53, 53, 59, 64, 64, 65, 66, 67, 67, 68, 71, 72, 75

i) Mean :

(40+46+51+52+53+53+53+59+64+64+65+66+67+67+68+71+72+75)/18

= 1086/18

= 60.33

ii) Median :

= (9^th value + 10^th value)/2

= (64 + 64)/2

= 64

iii) Mode :

Most repeated term is 53

So, mode is 53.

Problem 4 :

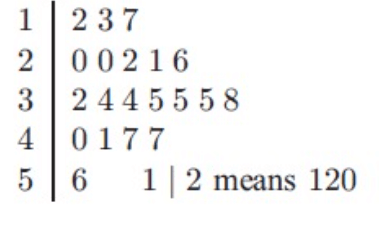
Find the data displayed in stem and leaf plot, find the

(i) Mean    (ii) Median and  (iii)  Mode

Solution :

120, 130, 170, 200, 200, 220, 210, 260, 320, 340, 340, 350, 350, 350, 380, 400, 410, 470, 470, 560

i) Mean :

Sum of numbers  =

(120+130+170+200+200+220+210+260+320+340+340+350+350+350+380+400+410+470+470+560)

= 6250/20

= 312.5

ii) Median :

= (10^th value + 11^th value)/2

= (340 + 340)/2

= 340

iii) Mode :

Most repeated term is 350

So, mode is 350.

Problem 5 :

The weight of the fish caught on a one day fishing trip are displayed in a stem and leaf plot shown. Find the median weight 

Solution :

Crossing out pairs from top and from bottom, the remaining quantities are 21 and 25

Average of 21 and 25 :

= (21 + 25)/2 = 46/2 = 23

So, median weight is 23 kg.