FIND THE LENGTH OF ARC CUTS OFF FROM A CIRCLE

Problem 1 :

Find the length of arc AB.

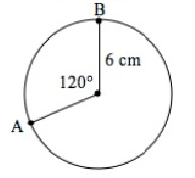
Solution :

Radius r = 6 cm

Central angle θ = 120^º

Length of arc AB = (θ/360) × 2πr

= (120/360) × 2 × 3.14 × 6

= 0.333 × 2 × 3.14 × 6

= 12.55 cm

So, the length of arc AB is 12.55 cm.

Problem 2 :

The diameter is 24 cm. Find the length of are CD.

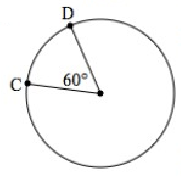
Solution :

Diameter D = 24 cm

Radius r = D/2

= 24/2

r = 12

Central angle θ = 60^º

Length of arc CD = (θ/360) × 2πr

= (60/360) × 2 × 3.14 × 12

= 0.1667 × 2 × 3.14 × 12

= 12.562 cm

So, the length of arc CD is 12.56 cm.

Problem 3 :

The length of arc EF is 5π in. Find the length of the radius.

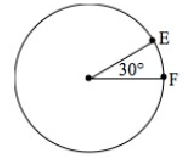
Solution :

The length of arc EF is 5π in.

Central angle θ = 30^º

Length of arc EF = (θ/360) × 2πr

5π = (30/360) × 2 × π × r

5 = 0.083 × 2 × r

5 = 0.166 × r

r = 5/0.166

r = 30.120

So, the length of arc EF is 30.120 cm.

Problem 4 :

Find the length of arc XY.

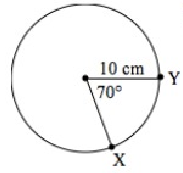
Solution :

Radius r = 10 cm

Central angle θ = 70^º

Length of arc XY = (θ/360) × 2πr

= (70/360) × 2 × 3.14 × 10

= 0.184 × 62,8

= 11.55 cm

So, the length of arc XY is 11.55 cm.

Find each measure. Give answers in terms of π and rounded to the nearest hundredth.

Problem 5 :

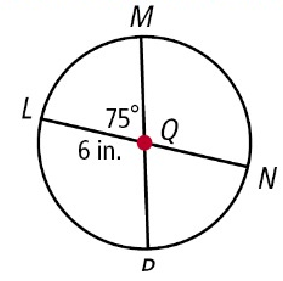
Area of sector LQM

Solution :

Radius r = 6 in

Central angle θ = 75^º

Area of a sector A = (θ/360) × πr²

= (75/360) × 3.14 × (6)²

= 0.2083 × 3.14 × 36

= 23.55 in².

So, the area of the sector is 23.55 in².

Problem 6 :

Length of arc ND

Solution :

Radius r = 6 cm

Central angle θ = 75^º

Length of arc NP = (θ/360) × 2πr

= (75/360) × 2 × 3.14 × 6

= 0.2083 × 37,68

= 7.85 

So, the length of arc NP is 7.85 in. 

Problem 7 :

The gear of a grandfather clock has a radius of 3 in. To the nearest tenth of an inch, what distance does the gear cover when it rotates through an angle of 88^º?

Solution :

Radius r = 3 in

Central angle θ = 88^º

A = (θ/360) × 2πr

= (88/360) × 2 × 3.14 × 3

= 0.244  × 18.84

= 4.6

So, the distance is 4.6 in.