FIND THE LEAST NUMBER TO BE ADDED TO GET A PERFECT SQUARE

Problem 1 :

The smallest number added to 680621 to make the sum a perfect square is :

(a) 4     (b)  5    (c)  6   (d) 8

Solution :

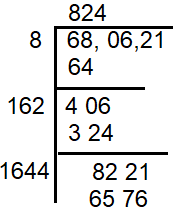
(825)² is the nearest perfect square.

825² = 825 x 825 ==> 680625

The difference between 680625 and 680621 is 

680625 - 680621 = 4

So, 4 should be added to the given number to get a perfect square.

Problem 2 :

What is the smallest number to be added to 1000 to make the resulting figure as perfect square.

Solution :

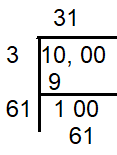
(32)² is the nearest perfect square.

32² = 32 x 32 ==> 1024

The difference between 1024 and 1000 is 

1024 - 1000 = 24

So, 24 should be added to the given number to get a perfect square.

Problem 3 :

If √1369 + √(0.0615) + x = 37.25, then x is equal to 

(a) 10^-1         (b) 10^-2           (c) 10^-3         (d) None

Solution :

√1369 + √(0.0615) + x = 37.25

37 + √(0.0615) + x = 37.25

√(0.0615) + x = 37.25 - 37

√(0.0615) + x = 0.25

Take square on both sides.

(0.0615) + x = (0.25)²

(0.0615) + x = (25/100)²

(0.0615) + x = (1/4) ⋅ (1/4)

0.0615 + x = 0.0625

x = 0.0625 - 0.0615

x = 0.001

x = 1/1000

x = 10^-3

Problem 4 :

The sum of two numbers is 22 and the sum of their square is 404, then the product of the numbers is 

Solution :

Let the two numbers be x and y.

x + y = 22

x² + y² = 404

(x + y)² = x² + y² + 2xy

Applying the given values, we get

(22)² = 404 + 2xy

484 = 404 + 2xy

2xy = 484 - 404

2xy = 80

xy = 80/2

xy = 40

Problem 5 :

Solution :