FIND THE IRRATIONAL NUMBER LOCATED THE NUMBER LINE

Name the point on the number line associated with each irrational number.

Problem 1 :

Locate √50 on the number line.

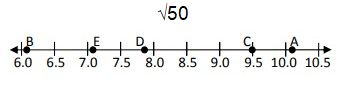
Solution :

√50 is lies between √49 and √64.

Approximate value of √50 is 7.07.

So, the number 7.07 is nearly connected to the point E.  

7.0 < 7.07 < 8.0

Problem 2 :

Locate √103 on the number line.

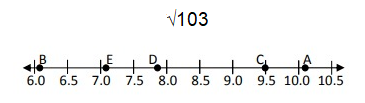
Solution :

√103 is lies between √100 and √121.

Approximate value of √103 is 10.1. So, point A will represent √103.

Problem 3 :

Locate √62 on the number line.

Solution :

√62

√62 is lies between √49 and √64.

Approximate value of √62 is 7.8.

So, the number 7.87 is nearly connected the point D.

7.0 < 7.87 < 8.0

Problem 4 :

Locate √90 on the number line.

 √90

√90 is lies between √81 and √100.

Approximate value of √90 is 9.48.

So, the number 9.48 is nearly connected the point C.  

9.5 < 9.48 < 10.0

Problem 5 :

Locate √37 on the number line.

√37 is lies between √36 and √49.

Approximate value of √37 is 6.0.

So, the number 6.08 is nearly connected the point B.  

6.0 < 6.08 < 7.0

Problem 6 :

Locate √7 on the number line.

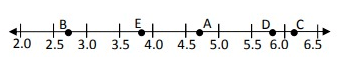
Solution :

√7

√7 is lies between √4 and √9.

Approximate value of √7 is 2.64.

So, the number 2.64 is middle the point B.  

2.8 < 2.64 < 3.8

Problem 7 :

Locate √22 on the number line.

√22 is lies between √16 and √25.

Approximate value of √22 is 4.69.

So, the number 4.69 is nearly connected to the point A.  

3.8 < 4.69 < 4.8

Problem 8 :

Locate √34 on the number line.

Solution :

√34

√34 is lies between √25 and √36.

Approximate value of √34 is 5.83.

So, the number 5.83 is nearly connected the point D.  

4.8 < 5.83 < 6.0

Problem 9 :

Locate √38 on the number line.

Solution :

√38

√38 is lies between √36 and √49.

Approximate value of √38 is 6.16. Point C will be the representation of 6.1

Problem 10 :

Locate √15 on the number line.

Solution :

√15

√15 is lies between √9 and √16.

Approximate value of √15 is 3.87.

So, the number 3.87 is nearly connected the point E.  

2.8 < 3.87 < 3.8