FIND THE INDICATED NTH ROOTS OF A

In general, for an integer n greater than 1, if bⁿ = a, then b is an nth root of a. An n^th root of a is written as ⁿ√a , where n is the index of the radical.

Let n be an integer (n > 1) and let a be a real number.

Find the indicated real n^th root(s) of a.

Problem 1 :

If n = 3, a = −216

Solution :

We can write the given details as cube root of -216. That is

= ∛-216

= ∛-6 ⋅ (-6) ⋅ (-6)

= -6

Problem 2 :

n = 4, a = 81

Solution :

Here n is even. So, we will have two solutions.

We can write the given details as fourth root of 81. That is,

= ∜81

= ∜(3 ⋅ 3 ⋅ 3 ⋅ 3)

= ±3

Problem 3 :

n = 4, a = 16

Solution :

Here n is even. So, we will have two solutions.

We can write the given details as fourth root of 81. That is,

= ∜16

= ∜(2 ⋅ 2 ⋅ 2 ⋅ 2)

= ±2

Problem 4 :

n = 2, a = −49

Solution :

Here n is even and value of a is less than 0. So, it will have no real roots.

Problem 5 :

n = 3, a = −125

Solution :

Here n is odd and value of a is less than 0. 

= ∛-125

= ∛-5 ⋅ (-5) ⋅ (-5)

= -5

Problem 6 :

n = 5, a = 243

Solution :

Here n is odd and value of a > 0. 

= 5^th root (243)

= 5^th root (3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)

= 3

Problem 7 :

Evaluate each expression.

a. 16^3/2          b. 32^−3/5

Solution :

a. 16^3/2 

= (2⁴)^3/2 

16 = 2

= 2^{4 x (3/2)}

= 2^{2 x 3}

= 2⁶

= 64

So, the value of 16^3/2 is 64.

b. 32^−3/5

32 = 2 x 2 x 2 x 2 x 2

= 2⁵

32^−3/5 = (2⁵)^−3/5

= 2^5(-3/5)

= 2^-3

= 1/2³

= 1/8

Problem 8 :

Find the real solution(s) of

(a) 4x⁵ = 128 and (b) (x − 3)⁴ = 625

Solution :

(a) 4x⁵ = 128

Dividing by 4

x⁵ = 128/4

x⁵ = 2⁵

Since the powers are the same, we 

x = 5

(b) (x − 3)⁴ = 625

(x − 3) = fourth root (625)

x - 3 = fourth root (5 x 5 x 5 x 5)

x - 3 = 5

x = 5 + 3

x = 8

Problem 9 :

Find the radius of the figure with the given volume

a)  V = 216 ft³

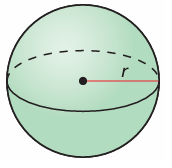
Solution :

Volume of sphere = (4/3) πr³

(4/3) πr³ = 216

r³ = 216 (3/4) x 1/π

r³ = 51.59

r = ∛51.59

r = 3.72

So, the required radius is 3.72 cm

b) V = 1332 cm³

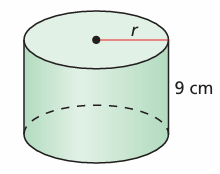
Solution :

Volume of cylinder= πr²h

1332 = πr²(9)

1332/9 = πr²

148 = πr²

148/3.14 = r² 

r² = 47.13

r = √47.13

r = 6.86

So, the radius of the cylinder is 6.86 cm.

Problem 10 :

A weir is a dam that is built across a river to regulate the flow of water. The flow rate Q (in cubic feet per second) can be calculated using the formula Q = 3.367ℓh^3/2, where ℓ is the length (in feet) of the bottom of the spillway and h is the depth (in feet) of the water on the spillway. Determine the flow rate of a weir with a spillway that is 20 feet long and has a water depth of 5 feet.

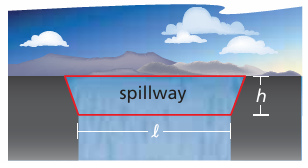
Solution :

Q = 3.367ℓh^3/2

Here l = 20 feet and h = 5 feet

Q = 3.367(20) (5)^3/2

= 3.367(20) (125)^1/2

= 67.34 (125)^1/2

= 67.34√125

= 67.34(11.18)

= 752.86 cubic feet per second

Problem 11 :

A hospital purchases an ultrasound machine for $50,000. The hospital expects the useful life of the machine to be 10 years, at which time its value will have depreciated to $8000. The hospital uses the declining balances method for depreciation, so the annual depreciation rate r (in decimal form) is given by the formula

r = 1 − [S/C]^1/n

In the formula, n is the useful life of the item (in years), S is the salvage value (in dollars), and C is the original cost (in dollars). What annual depreciation rate did the hospital use?

Solution :

The useful life is 10 years, so n = 10. The machine depreciates to $8000, so S = 8000. The original cost is $50,000, so C = 50,000. So, the annual depreciation rate is

r = 1 − [8000/50000]^1/10

r = 1 - (0.16)^0.1

= 1 - 0.83

= 0.167

Converting into percentage, we get

About 16.7%.