FIND THE INDICATED ANGLE IN THE PARALLELOGRAM WITH DIAGONALS

Find the measure of the indicated angle in each parallelogram.

Example 1 :

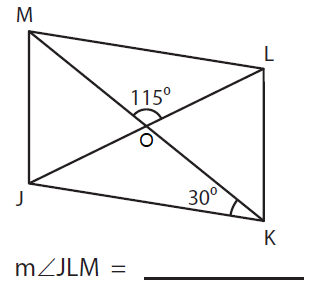
Solution :

In the given figure, ∠JKM = 30° and ∠MOL = 115°

By alternate angles,

∠JKM = ∠KML

30° = ∠KML

In ΔLOM,

We know that,

The sum of the interior angles of a triangle is 180°.

That is,

∠O + ∠M + ∠L = 180°

We have,

 ∠O = 115°, ∠M = 30°, and ∠L = ?

115° + 30° + ∠L = 180°

145° + ∠L = 180°

∠L = 180° - 145°

∠L = 35°

Now, ∠L = 35°. It is similar to m ∠JLM.

So, m ∠JLM = 35°

Example 2 :

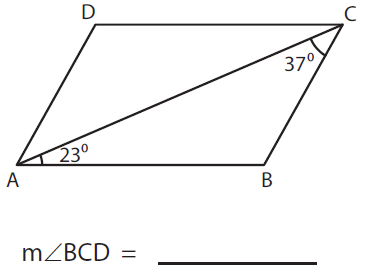
Solution :

In the given figure, ∠BAC = 23° and ∠BCA = 37°

By alternate angles,

∠BAC = ∠ACD

23° = ∠ACD

Now, ∠BCA = 37° and ∠ACD = 23°

To find ∠BCD,

∠BCD = ∠BCA + ∠ACD

= 37° + 23°

∠BCD = 60°

So, m ∠BCD = 60°.

Example 3 :

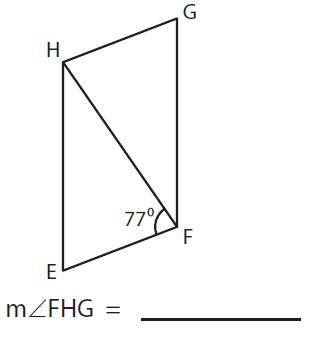
Solution :

In the given figure, ∠EFH = 77°

By alternate angles,

∠EFH = ∠FHG

77° = ∠FHG

So, m ∠FHG = 77°.

Example 4 :

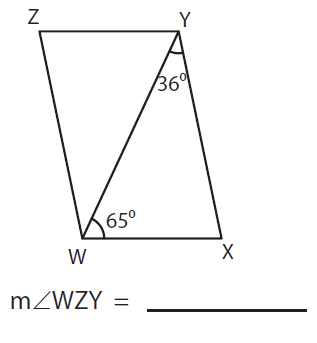
Solution :

In the given figure, ∠XWY = 65° and ∠XYW = 36°

By alternate angles,

In ΔWZY,

The sum of the interior angles of a triangle is 180°.

 ∠YWZ + ∠WYZ + ∠WZY = 180°

We have,

∠YWZ = 36°, ∠WYZ = 65°, and ∠WZY = ?

 36° + 65° + ∠WZY = 180°

101° + ∠WZY = 180°

∠WZY = 180° - 101°

∠WZY = 79°

So, m ∠WZY = 79°.

Example 5 :

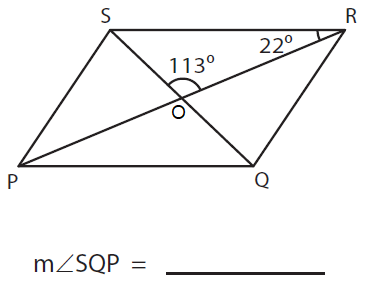
Solution :

In the given figure, ∠PRS = 22° and ∠SOR = 113°

By alternate angles,

∠PRS = ∠RPQ

22° = ∠RPQ = ∠OPQ

By vertically opposite angles,

∠SOR = ∠QOP

113° = ∠QOP

In ΔPOQ,

The sum of the interior angles of a triangle is 180°.

 ∠OPQ + ∠QOP + ∠OQP = 180°

We have,

∠OPQ = 22°, ∠QOP = 113°, and ∠OQP = ?

 22° + 113° + ∠OQP = 180°

135° + ∠OQP = 180°

∠OQP = 180° - 135°

∠OQP = 45° = ∠SQP

So, m ∠SQP = 45°.

Example 6 :

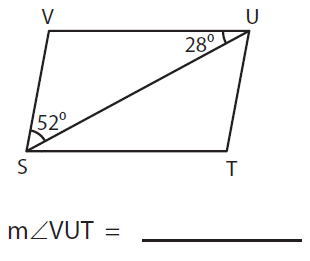
Solution :

In the given figure, ∠VSU = 52° and ∠VUS = 28°

By alternate angles,

∠VUS = ∠UST

28° = ∠UST

To find ∠VUT,

∠VUT = ∠VUS + ∠UST

= 52° + 28°

∠VUT = 80°

So, m ∠VUT = 80°.