FIND THE IMAGE OF THE LINE UNDER THE GIVEN TRANSLATION

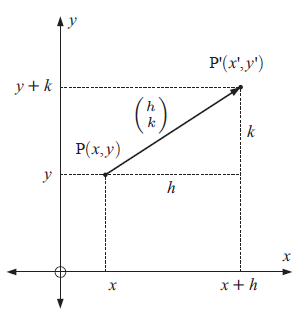
If P(x, y) is translated h units in the x-direction and k units in the y-direction to become P'(x', y'), then 

x' = x + h and y' = y + k

Find the image equation of the following and give answer in the form of y = f(x).

Problem 1 :

3x + 2y = 8 under (-1, 3)

Solution :

By observing the translation factor, h = -1 and k = 3. Moving the line left of 1 unit and up 3 units.

x' = x + h and y' = y + k

x' = x - 1 and y' = y + 3

Given equation :

3x + 2y = 8

3(x - 1) + 2(y + 3) = 8

3x - 3 + 2y + 6 = 8

3x + 2y + 3 = 8

3x + 2y + 3 - 8 = 0

After the translation, the required equation will be,

3x + 2y - 5 = 0

Problem 2 :

2x - y = 6 under (-3, 0)

Solution :

By observing the translation factor, h = -3 and k = 0. Moving the line left of 3 units and no vertical move.

x' = x + h and y' = y + k

x' = x - 3 and y' = y + 0

Given equation :

2x - y = 6

2(x - 3) - y = 6

2x - 6 - y = 6

2x - y = 6 + 6

2x - y = 12

After the translation, the required equation will be,

2x - y = 12

Problem 3 :

y = x² under (0, 3)

Solution :

By observing the translation factor, h = 0 and k = 3. There is no horizontal move and moving up 3 units.

x' = x + h and y' = y + k

x' = x + 0 and y' = y + 3

Given equation :

y = x²

y + 3 = (x+0)²

y + 3 = x²

y = x² + 3

After the translation, the required equation will be,

y = x² + 3

Problem 4 :

xy = 5 under (-4, 1)

Solution :

By observing the translation factor, h = -4 and k = 1. There is no horizontal move and moving up 1 unit.

x' = x + h and y' = y + k

x' = x - 4 and y' = y + 1

Given equation :

xy = 5

(x - 4)(y + 1) = 5

xy + x - 4y - 4 = 5

xy + x - 4y = 4 + 5

xy + x - 4y = 9

After the translation, the required equation will be,

xy + x - 4y = 9

Problem 5 :

y = 2^x under (0, -3)

Solution :

By observing the translation factor, h = 0 and k = -3. There is no horizontal move and moving up units.

x' = x + h and y' = y + k

x' = x - 0 and y' = y - 3

Given equation :

y = 2^x

y - 3 = 2^x

y = 2^x + 3

After the translation, the required equation will be,

y = 2^x + 3

Problem 6 :

y = 3^-x under (2, 0)

Solution :

By observing the translation factor, h = 2 and k = 0. We move horizontally 2 units right and no vertical move.

x' = x + h and y' = y + k

x' = x + 2 and y' = y - 0

Given equation :

y = 3^-x

y = 3^{-(x + 2)}

y = 3^{-x - 2}

y = 3^-x 3^-2

y = 3^-x / 9

y = 1/9(3^x)

After the translation, the required equation will be,

y = 1/9(3^x)

Problem 7 :

What single transformation is equivalent to a translation of (2, 1) followed by translation of (3, 4) ?

Solution :

Let us consider the point involving here as (x, y). Moving this point with the translation of (2, 1)

So, it will become (x + 2, y + 1)

Moving this point with (3, 4). Then, we have to move 3 unit right and 4 units up.

(x + 2 + 3, y + 1 + 4)

(x + 5, y + 5)

So, the single transformation is translation of (5, 5).

Problem 8 :

Complete the missing translation factor :

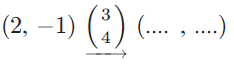
Solution :

Initial position is (2, -1).

Translation factor is (3, 4), we have to move the point 3 units right and 4 units up.

New position will be,

= (2 + 3, -1 + 4)

= (5, 3)

Problem 9 :

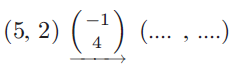
Solution :

Initial position is (5, 2).

Translation factor is (-1, 4), we have to move the point 1 unit left and 4 units up.

New position will be,

= (5 - 1, 2 + 4)

= (4, 6)

Problem 10 :

Solution :

Initial position is (3, -2).

Translation factor is unknown, let the translation factor be (h, k)

New position is (3, 1)

(2 + h, -2 + k) --> (3, 1)

2 + h = 3 and -2 + k = 1

h = 1 and k = 3

So, moving the point 1 unit right and 3 units up.

Problem 11 :

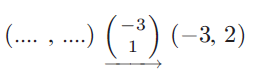
Solution :

Initial position is unknown, let the initial position be (x, y).

New position is (-3, 2)

(x - 3, y + 1) --> (-3, 2)

x - 3 = -3 and y + 1 = 2

x = 0 and y = 1

So, there is no horizontal move and vertically moving 1 unit up.