FIND THE HEIGHT OF A CONE GIVEN RADIUS AND SURFACE AREA

What is cone ?

A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.

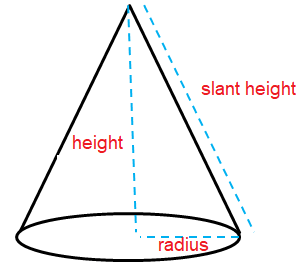
To find lateral surface area and total surface area of cone, we use the formulas given below.

Lateral surface area =  πrl

Total surface area =  πrl +  πr²

= πr(l + r)

l = √r² + h²

Here r = radius, l = slant height

Problem 1 :

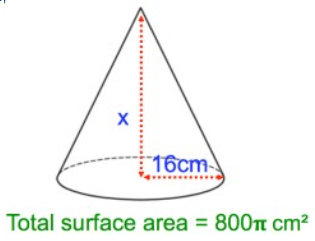
Solution :

Total surface area = 800π

πr(l + r) = 800π

Dividing by π on both sides, we get

r(l + r) = 800 ----(1)

From the given figure, r = 16 cm and h = x

l = √(16² + x²)

Applying the value of l in (1), we get

16(√(16² + x²) + 16) = 800

(√(16² + x²) + 16) = 50

√(16² + x²) = 50 - 16

√(16² + x²) = 34

Take square on both sides.

256 + x² = (34)²

256 + x² = 1156

x² = 1156 - 256

x² = 900

x = 30

Problem 2 :

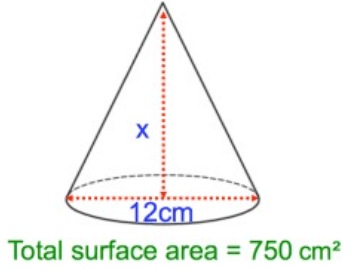
Solution :

Total surface area = 750

πr(l + r) = 750

Here π = 3.14, r = 6

3.14(6)(l + 6) = 750

l + 6 = 750/18.84

l + 6 = 39.80

l = √(6² + x²)

Applying the value of l, we get

√(6² + x²) + 6 = 39.80

√(6² + x²) = 33.80

Take square on both sides.

36 + x² = (33.80)²

36 + x² = 1142.44

x² = 1142.44 - 36

x² = 1106.44

x = 33.26

Problem 3 :

Find what length of canvas 3/4 m wide is required to make a conical tent 8 m in diameter and 3 m in high.

Solution :

Required quantity of canvas = Curved surface area of tent

length x width = πrl

Diameter = 8 m, r = 4 m, height = 3 m

l = √(r² + h²)

slant height (l) = √(4² + 3²)

l = √25

l = 5

length x (3/4) = 3.14(4)(5)

length x (3/4) = 62.8

length = 62.8(4/3)

length = 83.73

So, the required length of the canvas is 83.73 m.