FIND HEIGHT AND SLANT HEIGHT OF THE CONE WHEN SURFACE IS GIVEN

Find the slant height (h) and slant height (l) of the cone given below. Total surface area is given.

Problem 1 :

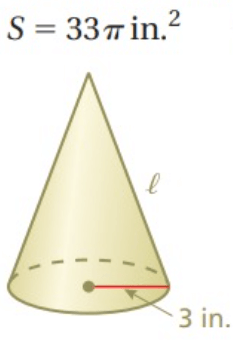
Solution :

Surface area of cone = 33π

π r(l + r) = 33π

Applying the value of r, we get

3(l + 3) = 33

Dividing by 3.

l + 3 = 11

Subtracting 3 on both sides.

l = 11 - 3

l = 8

h = √l² - r²

h = √8² - 3²

h = √(64 - 9)

h = √55

So, required height = √55 inches and slant height = 8 inches.

Problem 2 :

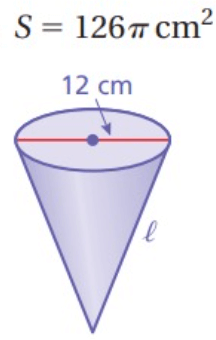
Solution :

Surface area of cone = 126π

Diameter = 12 cm

radius = 6 cm

π r(l + r) = 126π

Applying the value of r, we get

6(l + 6) = 126

Dividing by 6.

l + 6 = 21

Subtracting 6 on both sides.

l = 21 - 6

l = 15

h = √l² - r²

h = √15² - 6²

h = √(225 - 36)

h = √189

So, required height = 15 cm and slant height = √189 cm.

Problem 3 :

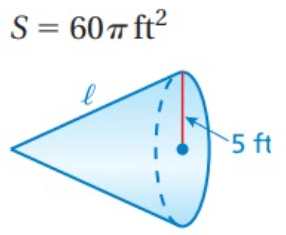
Solution :

Surface area of cone = π

radius = 5 ft

π r(l + r) = 60π

Applying the value of r, we get

5(l + 5) = 60

Dividing by 5.

l + 5 = 12

Subtracting 5 on both sides.

l = 21 - 5

l = 16

h = √16² - 5²

h = √256 - 25

h = √231

So, the required slant height is 16 ft and height is √231 ft.