FIND THE GREATEST NUMBER LEAVING THE REMAINDER WHILE DIVIDING

Problem 1 :

Find the largest number which divides 245 and 1029 leaving 5 in each case.

Solution :

By finding the greatest common divisor, we will get the number which will divide the given numbers 245 and 1029 without leaving any remainder.

So, let us reduce 5 in each case.

245 - 5 ==> 240

1029 - 5 ==> 1024

Now by finding the HCF of 240 and 1024, we will get the largest number which divides 240 and 1024 without leaving remainder.

But, when we divide 245 and 1029 by the HCF we will be getting 5 as remainder.

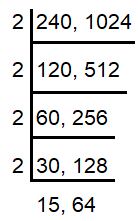
HCF (240, 1024) = 16

So, 16 is the greater number leaves the remainder 5 when we divide 245 and 1029.

Problem 2 :

Find the largest number which divides 2053 and 967 and leaves a remainder of 5 and 7 respectively.

Solution :

2053 - 5 ==>  2048

967 - 7 ==> 960

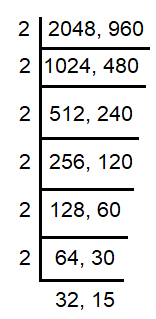
HCF (2048, 960) = 64

So, 64 is the greatest number which divides 2053 and 967 leaving the remainders 5 and 7 in each case.

Problem 3 :

Find the largest positive integer that will divide 398, 436 and 542 leaving remainder 7, 11 and 15 respectively.

Solution :

398 - 7 ==>  391

436 - 11 ==>  425

542 - 15 ==> 527

HCF (391, 425 and 527) :

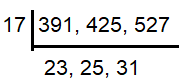
So, 17 is the largest number which will divide 398, 436, 542 by leaving the remainders 7, 11 and 15 respectively.