FIND THE FUNCTIONS F AND G FROM THE COMPOSITION FUNCTION

Find functions f and g so that f∘g = H

Problem 1 :

H(x) = (2x + 3)⁴

Solution :

Given that,

(f∘g)(x) = H (x)

= f [ g(x) ]

From this, we can understand that where we see x in the function f(x), it is being replaced by the function g(x).

Let g(x) = 2x + 3, then f(x) must be x⁴

Verifying our assumption :

= f(2x + 3)

= (2x + 3)⁴

So, the required functions f and g are

 f(x) = x⁴ and g(x) = 2x + 3

Problem 2 :

H(x) = (1+x²)³

Solution :

Given that,

(f∘g)(x) = H (x)

= f [ g(x) ]

One possible answer :

If g(x) = 1 + x², then  f(x) = x³

Other possible answers are also there :

If g(x) = x², then f(x) = (1 + x)³

Problem 3 :

H(x) = √(x² + 1)

Solution :

Given that,

(f∘g)(x) = H (x)

= f [ g(x) ]

One possible answer :

If g(x) = √(x + 1), then  f(x) = x²

Other possible answer :

If g(x) = √x, then  f(x) = x² + 1

Problem 4 :

H(x) = |2x + 1|

Solution :

Given that,

(f∘g)(x) = H (x)

= f [ g(x) ]

One possible answer :

If g(x) = |x|, then  f(x) = 2x + 1

One possible answer :

If g(x) = |x - 1|, then  f(x) = 2(x + 1)

Problem 5 :

H(x) = |2x² + 3|

Solution :

Given that,

(f∘g)(x) = H (x)

= f [ g(x) ]

One possible answer :

If g(x) = |2x+3|, then  f(x) = x²

Problem 6 :

Most functions are compositions of basic functions. Work backwards to determine the basic functions that created the composition

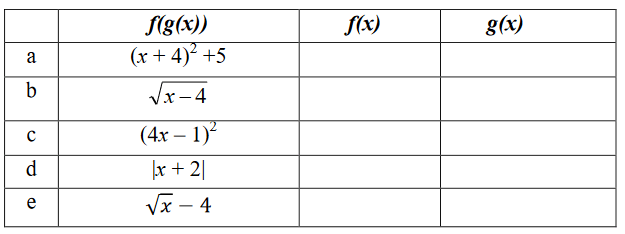
Solution :

Let H(x) = f(g(x))

a) f(g(x)) = (x + 4)² + 5

H(x) = (x + 4)² + 5

If f(x) = x² + 5 and g(x) = x + 4

b) f(g(x)) = √(x - 4)

H(x) = √(x - 4)

If g(x) = x - 4, then f(x) = √x

c) f(g(x)) = (4x - 1)²

H(x) = (4x - 1)²

If g(x) = 4x - 1, then f(x) = x²

d) f(g(x)) = |x + 2|

H(x) = |x + 2|

If g(x) = (x + 2), then f(x) = |x|

e) f(g(x)) = √x - 4

H(x) = √x - 4

If g(x) = √x, then f(x) = x - 4