FIND THE EQUATION OF THE TANGENT LINE TO THE CURVE AT THE GIVEN POINT

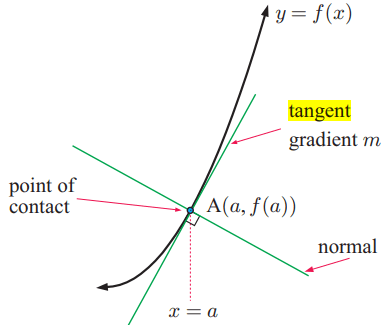
For each problem, find the equation of the line tangent to the function at the given point. Your answer should be in slope – intercept form.

Problem 1 :

y = x³ – 3x² + 2 at (3, 2)

Solution :

y = x³ – 3x² + 2

Differentiating with respect to x, we get

dy/dx = 3x² - 6x

Slope at (3, 2)

dy/dx = 3(3)² - 6(3)

dy/dx = 27 - 18

dy/dx = 9

Slope of tangent = 9

Equation of tangent :

(y - y₁) = m(x - x₁)

(y - 2) = 9(x - 3)

y - 2 = 9x - 27

y = 9x - 27 + 2

y = 9x - 25

Problem 2 :

Solution :

y = -5(x² + 1)^-1

Differentiating with respect to x, we get

dy/dx = -5(-1) (x² + 1)^-2 (2x)

dy/dx = 10x (x² + 1)^-2

Equation of tangent :

(y - y₁) = m(x - x₁)

Problem 3 :

y = x³ – 2x² + 2 at (2, 2)

Solution :

y = x³ – 2x² + 2

Differentiating with respect to x, we get

dy/dx = 3x² - 4x

Slope at (2, 2)

dy/dx = 3(2)² - 4(2)

dy/dx = 12 - 8

dy/dx = 4

Slope of tangent = 4

Equation of tangent :

(y - y₁) = m(x - x₁)

(y - 2) = 4(x - 2)

y - 2 = 4x - 8

y = 4x - 8 + 2

y = 4x - 6

Problem 4 :

Solution :

y = -3(x² - 25)^-1

Differentiating with respect to x, we get

dy/dx = -3(-1) (x² - 25)^-2 (2x)

dy/dx = 6x (x² - 25)^-2

Equation of tangent :

(y - y₁) = m(x - x₁)

Problem 5 :

Solution :

y = -3(x² - 4)^-1

Differentiating with respect to x, we get

dy/dx = -3(-1) (x² - 4)^-2 (2x)

dy/dx = 6x (x² - 4)^-2

Equation of tangent :

(y - y₁) = m(x - x₁)

Problem 6 :

Solution :

Differentiating with respect to x, we get

Equation of tangent :

(y - y₁) = m(x - x₁)

Problem 7 :

y = In (-x) at (-2, In 2)

Solution :

y = In (-x)

Differentiating with respect to x, we get

dy/dx = -1/-x

dy/dx = 1/x

Slope at (-2, In 2)

dy/dx = 1/-2

dy/dx = -1/2

Slope of tangent = -1/2

Equation of tangent :

(y - y₁) = m(x - x₁)

(y - In 2) = -1/2(x + 2)

(y - In 2) = -1/2 x - 2/2

y - In 2 =  -1/2 x - 1

y = -1/2 x + In 2 - 1

Problem 8 :

y = -2tan (x) at (-π, 0)

Solution :

y = -2tan (x)

Differentiating with respect to x, we get

dy/dx = -2 ⋅ sec²(x)

Slope at (-π, 0)

dy/dx = -2 ⋅ sec²(-π)

= -2 ⋅ 1

= -2

Slope of tangent = -2

Equation of tangent :

(y - y₁) = m(x - x₁)

y  - 0 = -2(x + π )

y - 0 = -2x - 2π

y = -2x - 2π