FIND THE EQUATION OF QUADRATIC FUNCTION FROM A GRAPH

The quadratic function which is in the standard form will be

y = ax² + bx + c

this will have two roots α and β.

Roots = zeroes = x-intercepts

To find quadratic function from the given roots, we follow the steps give below.

Step 1 :

From the given graph, mark the zeroes and write them as values of x and convert it into factored form.

x = α ==> (x - α) (factor)

x = β ==> (x - β) (factor)

y = a(x - α)(x - β)

Step 2 :

To figure out the value of a, we will get one more point from the graph given except zeroes.

(i) It may be maximum or minimum point or y-intercept.

(ii) Mark it as point and apply in the quadratic function

(iii) Figure the value of a and simplify.

Determine the equation of quadratic function from graph. Give the function in general form.

Example 1 :

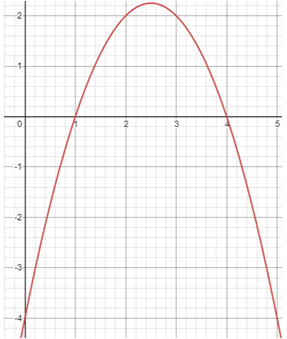
Solution :

From the graph, x-intercepts are 1 and 4.

So, x = 1 and x = 4

Factored form :

y = a(x - 1)(x - 4)

By observing the graph, the parabola cuts the y-axis at -4. By writing it as point (0, -4).

-4 = a(0 - 1)(0 - 4)

-4 = a(-1)(-4)

-4 = 4a

a = -1

y = -1(x - 1)(x - 4)

y = -1(x² - 5x + 4)

y = -x² + 5x - 4

Here the coefficient of x² is -1, from the graph we have evidence that the parabola opens down.

Example 2 :

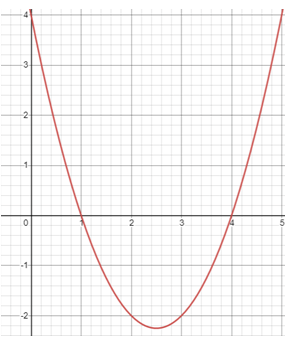
Solution :

From the graph, x-intercepts are 1 and 4.

So, x = 1 and x = 4

Factored form :

y = a(x - 1)(x - 4)

By observing the graph, the parabola cuts the y-axis at -4. By writing it as point (0, 4).

4 = a(0 - 1)(0 - 4)

4 = a(-1)(-4)

4 = 4a

a = 1

y = 1(x - 1)(x - 4)

y = 1(x² - 5x + 4)

y = x² - 5x + 4

Here the coefficient of x² is 1, from the graph we have evidence that the parabola opens up.

Example 3 :

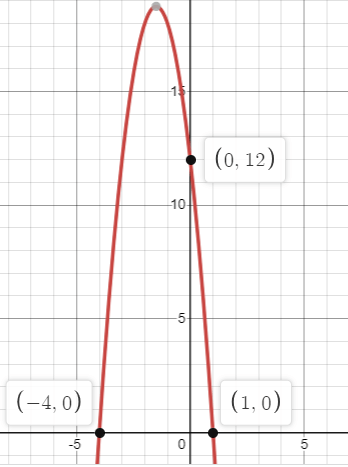
Solution :

From the graph, x-intercepts are -4 and 1.

So, x = -4 and x = 1

Factored form :

y = a(x + 4)(x - 1)

By observing the graph, the parabola cuts the y-axis at 12. By writing it as point (0, 12).

12 = a(0 + 4)(0 - 1)

12 = -4a

a = -3

y = -3(x + 4)(x - 1)

y = -3(x² + 3x - 4)

y = -3x² - 9x + 12

Here the coefficient of x² is -3, from the graph we have evidence that the parabola opens down.

Example 4 :

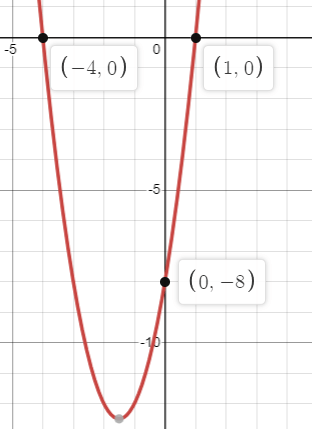
Solution :

From the graph, x-intercepts are -4 and 1.

So, x = -4 and x = 1

Factored form :

y = a(x + 4)(x - 1)

By observing the graph, the parabola cuts the y-axis at -8. By writing it as point (0, -8).

-8 = a(0 + 4)(0 - 1)

-8 = -4a

a = 2

y = 2(x + 4)(x - 1)

y = 2(x² + 3x - 4)

y = 2x² + 6x - 8

Here the coefficient of x² is 2, from the graph we have evidence that the parabola opens up.

Example 5 :

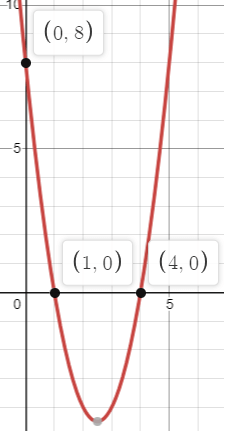
Solution :

From the graph, x-intercepts are 4 and 1.

So, x = 4 and x = 1

Factored form :

y = a(x - 4)(x - 1)

By observing the graph, the parabola cuts the y-axis at -8. By writing it as point (0, 8).

8 = a(0 - 4)(0 - 1)

8 = 4a

a = 2

y = 2(x - 4)(x - 1)

y = 2(x² - 5x + 4)

y = 2x² - 10x + 8

Here the coefficient of x² is 2, from the graph we have evidence that the parabola opens up.

FIND THE EQUATION OF QUADRATIC FUNCTION FROM A GRAPH

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling