FIND THE EQUATION OF A TRANSFORMED QUADRATIC FUNCTION FROM A GRAPH

y = a(x - h)² + k

is the equation of parabola which is having the vertex (h, k)

The sign of a will decide if there is any reflection or not.

• The sign of a is positive, the parabola will open up
• The sign of a is negative, the parabola will open down.

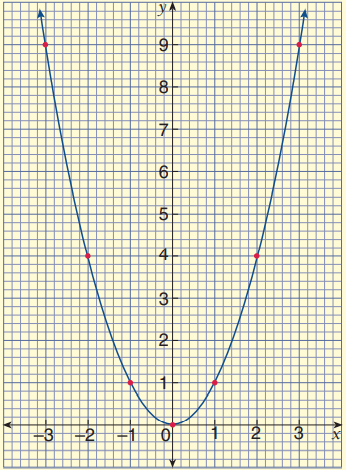
The parabolas shown are the result of translating and/or reflecting the parabola y = x². Find the equation of each parabola.

Problem 1 :

Solution :

Since the parabola opens down, there is a reflection.

a = -1

Horizontally the graph of y = -x² is not moved.

Vertically the graph of y = -x² is moved 4 units up.

h = 0 and k = 4

y = -1(x - 0)² + 4

So, the equation from the given graph is 

y = -1x² + 4

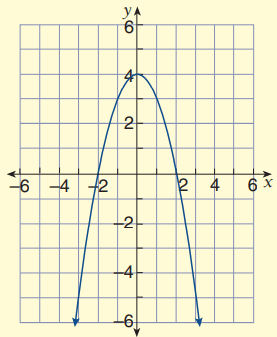
Problem 2 :

Solution :

Since the parabola opens down, there is no reflection.

a = 1

Horizontally the graph of y = x² is moved 3 units to the left.

Vertically the graph of y = -x² is not moved.

h = -3 and k = 0

y = 1(x - (-3))² + 0

So, the equation from the given graph is 

y = (x + 3)²

Problem 3 :

Solution :

Since the parabola opens down, there is reflection.

a = -1

Horizontally the graph of y = -x² is moved 3 units to the right.

Vertically the graph of y = -x² is moved 3 units up.

h = 3 and k = 3

y = -1(x - 3)² + 3

So, the equation from the given graph is 

y = -(x - 3)² + 3

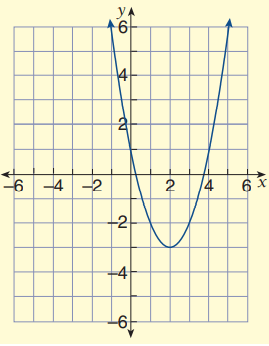
Problem 4 :

Solution :

Since the parabola opens down, there is no reflection.

a = 1

Horizontally the graph of y = x² is moved 2 units to the right.

Vertically the graph of y = x² is moved 3 units down.

h = 2 and k = -3

y = 1(x - 2)² - 3

So, the equation from the given graph is 

y = 1(x - 2)² - 3

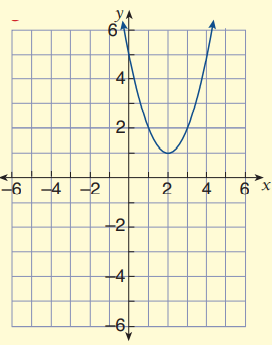
Problem 5 :

Solution :

Since the parabola opens down, there is no reflection.

a = 1

Horizontally the graph of y = x² is moved 2 units to the right.

Vertically the graph of y = x² is moved 1 unit up.

h = 2 and k = 1

y = 1(x - 2)² + 1

So, the equation from the given graph is 

y = (x - 2)² + 1

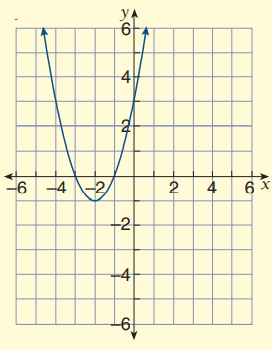
Problem 6 :

Solution :

Since the parabola opens down, there is no reflection.

a = 1

Horizontally the graph of y = x² is moved 2 units left.

Vertically the graph of y = x² is moved 1 unit down.

h = -2 and k = -1

y = 1(x - (-2))² - 1

So, the equation from the given graph is 

y = (x + 2)² - 1