FIND THE DISTANCE OF CHORD FROM THE CENTER

Problem 1 :

A circle of 30 cm diameter has a 24 cm chord what is the distance of the chord from the center?

Solution :

Diameter of circle = 30 cm, radius = 15 cm

Chord length = 24 cm

Let us draw the picture to represent the given situation.

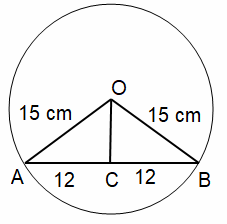
By drawing the perpendicular from the center to chord, it will bisect the chord into two equal parts.

Triangle OCB must be a right triangle.

By using Pythagoras theorem,

OC = √OB² - BC²

 OC = √15² - 12²

 OC = √225 - 144

OC = √81

OC = 9

So, distance from center to chord is 9 cm.

Problem 2 :

A chord AB of a circle with center O is 10 cm. if the chord is 12 cm away the center, then what is the radius of the circle?

Solution :

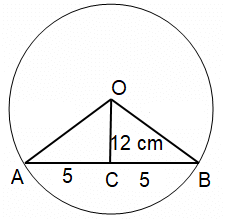
Chord AB = 10 cm, then BC = 5 cm and OB = r

OC ⊥ AB

By using Pythagoras theorem,

OB² = OC² + BC²

r² = 12² + 5²

r² = 144 + 25

r² = 169

r = √169

r = 13 cm

So, the radius of the circle is 13 cm.

Problem 3 :

If the diameter AD of a circle is 34 cm and the length of a chord AB is 30 cm. what is the distance of AB from the center?

Solution :

Let O be the center of the circle.

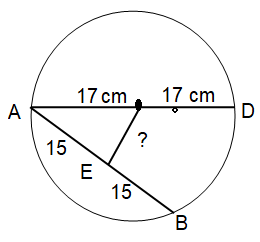
In right angled triangle AOB, by using Pythagoras theorem,

AO² = AE² + EO²

17² = 15² + EO²

OE² = 17² - 15²

OE² = 289 - 225

OE² = 64

OE = 8 cm

So, the distance of AB from the center of circle is 8 cm.

Problem 4 :

What is the length of a chord which is at a distance of 4 cm from the center of a circle of radius 5 cm?

Solution:

Distance of the chord from the center = 4 cm

Radius of the circle = 5 cm

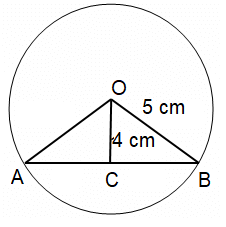
 OB² = OC² + BC²

5² = 4² + BC²

BC² = 5² - 4²

BC²= 25 - 16

BC² = 9

BC = 3 cm

AB = 2BC

AB = 2(3)  ==> 6 cm

So, the length of a chord is 6 cm.

Problem 5 :

If the radius of a circle is 13 cm and the length of its chord is 10 cm then what is the distance of chord from the center?

Solution :

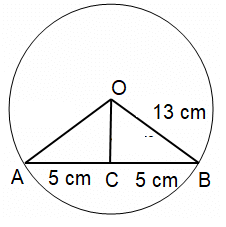
Radius of a circle = 13 cm

Length of its chord = 10 cm

= 10/2 = 5 cm

Distance = √r² - l²

 Distance = √13² - 5²

 = √169 - 25

 = √144

= 12 cm

So, the distance of the chord is 12 cm.

Problem 6 :

If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is:

Solution :

AB = 12 cm, BC = 16 cm

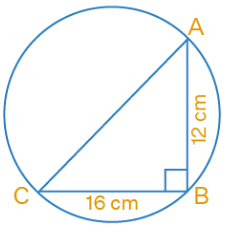
BC is perpendicular to AB which means that AC is the diameter.

In triangle ABC,

AC² = AB² + BC²

AC² = 12² + 16²

AC² = 144 + 256

AC² = 400

AC = 20 cm

Radius of circle = 1/2 × AC

= 1/2 × 20

= 10 cm

So, the radius of the circle is 10 cm.