FIND THE DETAILS FROM THE BOX AND WHISKER PLOT

Problem 1 :

For each box plot below, find the

(i) median, (ii) Interquartile range, (iii) range

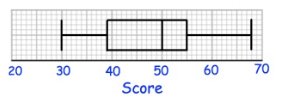
Solution :

(i)           Median

Median = 50 score

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 55 - 39

Interquartile range = 16

(iii)        Range

Range = Largest value - smallest value

= 68 - 30

Range = 38 score

Problem 2 :

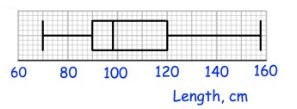
Solution :

(i)           Median

Median = 98

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 120 - 90

Interquartile range = 30

(iii)        Range

Range = Largest value - smallest value

= 158 - 70

Range = 88 cm

Problem 3 :

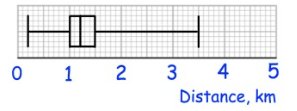
Solution :

(i)           Median

Median = 1.2

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 1.5 - 1

Interquartile range = 0.5

(iii)        Range

Range = Largest value - smallest value

= 3.5 - 0.2

Range = 3.3 km

Problem 4 :

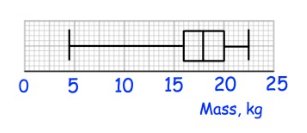
Solution :

(i)           Median

Median = 18

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 20 - 16

Interquartile range = 4

(iii)        Range

Range = Largest value - smallest value

= 22.5 - 4.5

Range = 18 kg

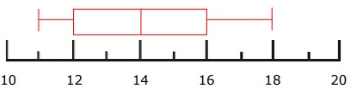
Solution :

(i)           Median

Median = 14

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 17 - 12

Interquartile range = 5

(iii)        Range

Range = Largest value - smallest value

= 19 - 10

Range = 9

Problem 6 :

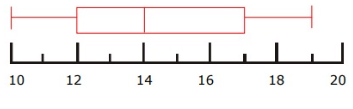
Solution :

(i)           Median

Median = 36

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 38 - 32

Interquartile range = 6

(iii)        Range

Range = Largest value - smallest value

= 39 - 31

Range = 8

Problem 7 :

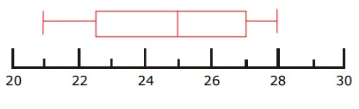
Solution :

(i)           Median

Median = 25

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 27 - 22.5

Interquartile range = 4.5

(iii)        Range

Range = Largest value - smallest value

= 28 - 21

Range = 7

Problem 8 :

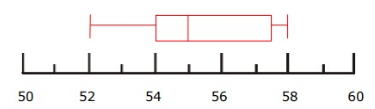
Solution :

(i)           Median

Median = 55

(ii)          Interquartile range

Interquartile range = Q₃ - Q₁

= 57.5 - 54

Interquartile range = 3.5

(iii)        Range

Range = Largest value - smallest value

= 58 - 52

Range = 6