FIND SURFACE AREA AND VOLUME OF SIMILAR SOLIDS

If two figures are similar then:

• the figures are equiangular, and
• the corresponding sides are in proportion.

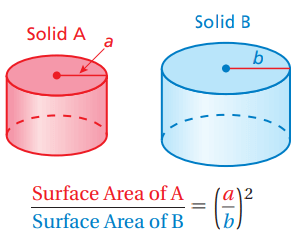
Surface area of similar figures :

If two solids are similar, then the ratio of their surface areas is equal to the square of the ratio of their corresponding linear measures. 

Volume of similar figures :

If two solids are similar, then the ratio of their volumes is equal to the cube of the ratio of their corresponding linear measures.

The scale factor between two similar figures is given. The surface area and volume of the smaller figure are given. Find the surface area and volume of the larger figure.

Problem 1 :

Scale factor = 1 : 2

SA = 90 yd²

V = 216 yd³

Solution :

Scale factor (k) = 1 : 2 = 1/2

i)  Surface area of smaller figure / surface area of larger

= (1/2)²

Surface area of smaller figure = 90 yd²

90/Surface area of larger figure = (1/4)

Surface area of larger figure = 90(4)

= 360 yd²

So, surface area of larger figure is 360 yd².

ii)  Volume of smaller figure / Volume of larger = (1/2)³

Volume of smaller figure = 216 yd³

216/volume of larger figure = (1/8)

Volume of larger figure = 216(8)

= 1728 yd³

So, volume of larger figure is 1728 yd³.

Problem 2 :

Scale factor = 4 : 9

SA = 256 km²

V = 1536 km³

Solution :

i)  Surface area of smaller figure / surface area of larger

= (4/9)²

Surface area of smaller figure = 256 km²

256/Surface area of larger figure = (4/9)²

Surface area of larger figure = 256(81/16)

= 1296 yd²

So, surface area of larger figure is 1296 yd².

ii)  Volume of smaller figure / Volume of larger = (4/9)³

Volume of smaller figure = 1536 yd³

1536/volume of larger figure = (64/729)

Volume of larger figure = 1536(729/64)

= 17496 km³

So, volume of larger figure is 17496 km³.

Problem 3 :

The dimensions of the touch tank at an aquarium are doubled. What is the volume of the new touch tank?

A) 150 ft³       B) 4000 ft³    C) 8000 ft³    D) 16,000 ft³ 

Solution :

The dimensions are doubled, so the ratio of the dimensions in the original tank to the dimensions in the new tank is 1 : 2.

(Original volume/new volume) = (original dimension/new dimension)³

(2000/new volume)= (1/2)³

(2000/new volume)= (1/8)

New volume = 2000(8)

= 16000 ft³

The solids are similar. Find the volume of the red solid. Round your answer to the nearest tenth.

Problem 4 :

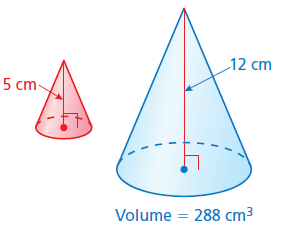
Solution :

Scale factor (k) = 5/12

Volume of red solid / volume of blue solid = k³

Volume of red solid / 288 = (5/12)³

Volume of red solid / 288 = 125/1728

Volume of red solid = (125/1728)⋅288

= 20.8 cm³

Problem 5 :

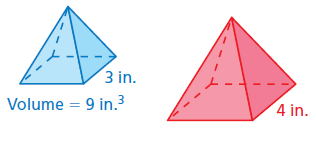
Solution :

Scale factor (k) = 3/4

Volume of blue solid / volume of red solid = k³

9 / Volume of red solid = (3/4)³

9 / Volume of red solid = (27/64)

Volume of red solid = 9(64/27)

= 21.3 in³