FIND RADIUS OF CIRCLE FROM THE GIVEN AREA OF SECTOR
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is area of sector ?
A section of a circle determined by a central angle and a corresponding circular arc.
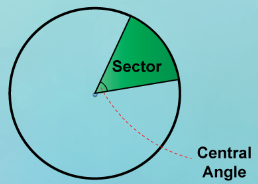
To find area of sector, we use the formula
A = (θ/360˚) ∙ πr²
Problem 1 :
A sector of a circle has central angle 45 and area 49π/8 cm². Find the radius of the circle.
Solution :
The formula to find area of the sector is
A = (θ/360˚) ∙ πr²
Substitute θ = 45˚ and area = 49π/8 cm²
49π/8 = 45/360 ∙ πr²
49π/8 = 1/8 ∙ πr²
πr² = (49π/8) × 8
r² = 49
r = √49
r = 7 cm
So, the radius of the circle is 7 cm.
Problem 2 :
A sector of a circle has central angle 150 and area 5π/27 ft². Find the radius of the circle.
Solution :
The formula to find area of the sector is
A = (θ/360˚) ∙ πr²
Substitute θ = 150˚ and area = 5π/27 ft²
5π/27 = 150/360 ∙ πr²
5π/27 = 5/12 ∙ πr²
πr² = 5π/27 × 12/5
r² = 4/9
r = √4/9
r = 2/3
r = 0.6 ft
So, the radius of the circle is 0.6 ft.
Problem 3 :
A sector of a circle has central angle 120˚ and area 16π/75 in². Find the radius of the circle.
Solution :
The formula to find area of the sector is
A = (θ/360˚) ∙ πr²
Substitute θ = 120˚ and area = 16π/75 in²
16π/75 = 120/360 ∙ πr²
16π/75 = 1/3 ∙ πr²
πr² = 16π/75 × 3
r² = 16/25
r = √16/25
r = 4/5
r = 0.8 in
So, the radius of the circle is 0.8 in.
Problem 4 :
A sector of a circle has central angle 210˚ and area 21π/4 m². Find the radius of the circle.
Solution :
The formula to find area of the sector is
A = (θ/360˚) ∙ πr²
Substitute θ = 210˚ and area = 21π/4 m²
21π/4 = 210/360 ∙ πr²
21π/4 = (7/12) ∙ πr²
πr² = (21π/4) × 12/7
r² = 9
r = √9
r = 3 m.
So, the radius of the circle is 3 m.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling