FIND MISSING VERTEX OF 2D SHAPES IN COORDINATE GEOMETRY

Problem 1 :

Points P(4, 12), Q(9, 14), and R(13, 4) are three vertices of a rectangle. Find the coordinates of the fourth vertex S.

Solution:

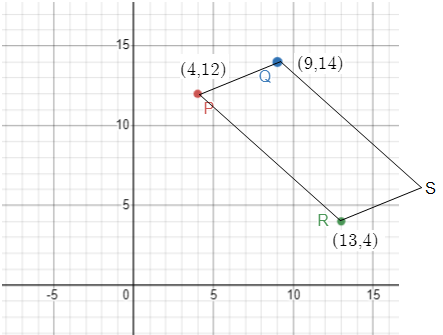
Let the coordinate of the fourth vertex are S(a, b).

Midpoint of PR = Midpoint of QS

On comparing both sides,

So, the coordinates of the fourth vertex are (8, 2).

Problem 2 :

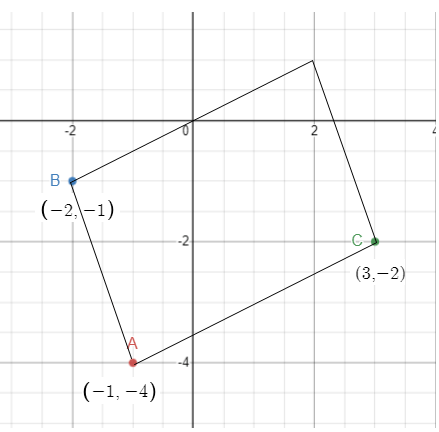
Find point D that makes ABCD a square where A(-1, 4), B(-2, -1), and C(3, -2).

Solution:

Let the coordinate of the fourth vertex are D(a, b).

Midpoint of AC = Midpoint of BD       

So, the coordinates of the fourth vertex are (4, 3).

Problem 3 :

Points A(-1, 2), B(-3, -3) and D(6, 3) form three corners of a parallelogram. Find the fourth vertex, C.

Solution:       

Let the coordinate of the fourth vertex are C(a, b).

Midpoint of AC = Midpoint of BD 

So, the coordinates of the fourth vertex are (4, -2).

Problem 4 :

Find point P that makes PQRS a rectangle where Q(-1, -5), R(2, -3) and S(-2, 3).

Solution:

Let the coordinate of the fourth vertex are P(a, b).

Midpoint of PR = Midpoint of QS

So, the coordinates of the fourth vertex are (-5, 1).

Problem 5 :

Find point S that makes PQRS a rectangle where P(6, 36), Q(-30, 9), and R(-12, -15).

Solution:

Let the coordinate of the fourth vertex are S(a, b).

Midpoint of PR = Midpoint of QS