FIND MISSING VALUES IN POLYGON

The polygons are regular. Find the value of x.

Problem 1 :

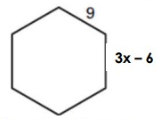
Solution :

Regular polygons :

If all the sides and interior angles of the polygons are equal.

3x - 6 = 9

3x = 9 + 6

3x = 15

x = 15/3

x = 5

Problem 2 :

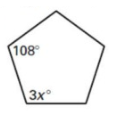
Solution :

3x = 108^º

x = 108^º/3

x = 36^º

Problem 3 :

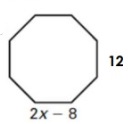
Solution :

2x - 8 = 12

2x = 12 + 8

2x = 20

x = 20/2

x = 10

Find the sum of the measures of the interior angles of the convex polygon with n sides.

Problem 4 :

n = 5

Solution :

Sum of all interior angles = (n - 2) × 180^º

= (5 - 2) × 180^º

= 3 × 180^º

= 540^º

Problem 5 :

n = 7

Solution :

Sum of all interior angles = (n - 2) × 180^º

= (7 - 2) × 180^º

= 5 × 180^º

= 900^º

Problem 6 :

n = 9

Solution :

Sum of all interior angles = (n - 2) × 180^º

= (9 - 2) × 180^º

= 7 × 180^º

= 1260^º

Find angle A.

Problem 7 :

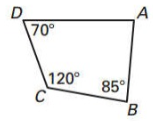
Solution :

The sum of the interior angles of a trapezoid equals 360^º, and the angles on each side of the trapezoid are supplementary.

Let A = x

x + 70^º + 120^º + 85^º = 360^º

x + 275^º = 360^º

x = 360^º - 275^º

x = 85^º

So, the values of A is 85^º.

Problem 8 :

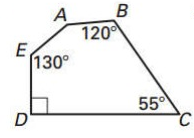
Solution :

Let A = x

x + 120^º + 55^º + 130^º + 90^º = 540^º

x + 395^º = 540^º

x = 540^º - 395^º

x = 145^º

So, the values of A is 145^º.

Problem 9 :

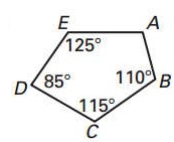
Solution :

Let A = x

x + 110^º + 115^º + 85^º + 125^º   = 540^º

x + 435^º = 540^º

x = 540^º - 435^º

x = 105^º

So, the values of A is 105^º.

Find the measure of an interior angle of the regular polygon.

Problem 10 :

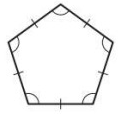
Solution :

Interior angle of the regular polygon = [(n - 2) × 180^º]/n

= [(5 - 2) × 180^º]/5

= [3 × 180^º]/5

= 540^º/5

= 108^º

Problem 11 :

Regular heptagon

Solution :

A heptagon is a seven-sided polygon.

So, n = 7

Interior angle of the regular polygon = [(n - 2) × 180^º]/n

= [(7 - 2) × 180^º]/7

= [5 × 180^º]/7

= 900^º/7

= 128.6^º

Problem 12 :

Regular 11-gon

Solution :

 n = 11

Interior angle of the regular polygon = [(n - 2) × 180^º]/n

= [(11 - 2) × 180^º]/11

= [9 × 180^º]/11

= 1620^º/11

= 147.3^º