FIND MISSING SIDE PERIMETER WITH POLYNOMIALS

Problem 1 :

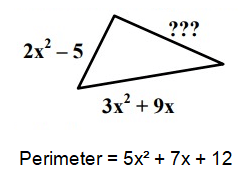
Solution :

Let, missing side = S

2x² - 5 + 3x² + 9x + S = 5x² + 7x + 12

5x² + 9x – 5 + S = 5x² + 7x + 12

S = 5x² + 7x + 12 – 5x² - 9x + 5

S = - 2x + 17

Problem 2 :

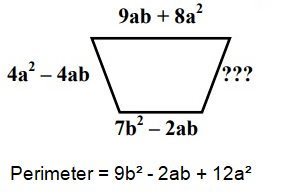
Solution:

Let, missing side = S

7b² – 2ab + 4a² - 4ab + 9ab + 8a² + S = 9b² - 2ab + 12a²

12a² + 7b² + 3ab + S = 9b² - 2ab + 12a²

S = 9b² - 2ab + 12a² - 12a² - 7b² - 3ab

S = 2b² - 5ab

Problem 3 :

Solution :

Let, missing side = S

2(5x² - 3x + 2) + 2S = 14x² + 4x - 8

10x² - 6x + 4 + 2S = 14x² + 4x - 8

2S = 14x² + 4x – 8 – 10x² + 6x – 4

2S = 4x² + 10x – 12

S = 4x² + 10x – 12

Problem 4 :

The measure of the perimeter of a triangle is 37s + 42. It is known that two of the sides of the triangle have measures of 14s + 16 and 10s + 20. Find the length of the third side.

Solution :

Perimeter of a triangle = 37s + 42

Length of the first side (a) = 14s + 16

Length of the second side (b) = 10s + 20

To find, third side (c)

Perimeter = a + b + c

37s + 42 = 14s + 16 + 10s + 20 + third side

37s + 42 = 24s + 36 + third side

Third side = 37s + 42 – 24s – 36

Third side = 13s + 6

So, the length of the third side is 13s + 6.

Problem 5 :

A triangle has a perimeter of 10a + 3b + 12 and has sides of length 3a + 8 and 5a + b, what is the length of the third side?

Solution :

Perimeter of a triangle = 10a + 3b + 12

Length of the first side = 3a + 8

Length of the second side = 5a + b

To find, third side (c)

Perimeter = a + b + c

10a + 3b + 12 = 3a + 8 + 5a + b + third side

Third side = 10a + 3b + 12 - 3a - 8 - 5a - b

Third side = 2a + 2b + 4

So, the length of the third side is 2a + 2b + 4.

Problem 6 :

For a rectangle with length of 3x + 4 and perimeter of 10x + 18, what is the width of the rectangle?

Solution :

Perimeter of a rectangle = 3x + 4

Length of a rectangle = 3x + 4

Perimeter of a rectangle = 2(l + w)

To find, width (w)

10x + 18 = 2(3x + 4 + w)

10x + 18 = 2(3x + 4) + 2(w)

10x + 18 = 6x + 8 + 2w

2w = 10x + 18 – 6x – 8

2w = 4x + 10

w = (4x + 10) / 2

w = 2x + 5

So, width of the rectangle is 2x + 5.

Problem 7 :

A rectangle has a perimeter of 12y² - 2y + 18 and has a width of 4y² - y + 6. What is the length of the rectangle?

Solution :

Perimeter of a rectangle = 12y² - 2y + 18

Width of a rectangle = 4y² - y + 6

Perimeter of a rectangle = 2(l + w)

To find, length (l)

12y² - 2y + 18 = 2(l + 4y² - y + 6)

12y² - 2y + 18 = 2(l) + 2(4y² - y + 6)

12y² - 2y + 18 = 2l + 8y² - 2y + 12

2l = 12y² - 2y + 18 – 8y² + 2y – 12

2l = 4y² + 6

l = 2y² + 3

So, length of the rectangle is 2y² + 3.