FIND MISSING COORDINATE IN COORDINATE GEOMETRY WORKSHEET

Problem 1 :

For what value of x are the points

A(-3, 12), B(7, 6) and C(x, 9)

collinear ?

a)1       b) -1     c) 2      d) -2

Solution

Problem 2 :

For what value of y are the points

A(1, 4), B(3, y) and C(-3, 16)

collinear ?

a)1      b) -1     c) 2     d) -2

Solution

Problem 3 :

Find the value of p for which the points

A(-1, 3), B(2, p) and C(5, -1)

collinear ?

a)1      b) -1      c) 2       d) -2

Solution

Problem 4 :

If the points

(1, x), (5, 2) and (9, 5)

are collinear then the value of x is

a) 5/2     b) -5/2     c) -1     d) 1

Solution

Problem 5 :

If the points (-1, 1), (2, p) and (8, 11) are collinear, find the value of p using section formula.

Solution

Problem 6 :

If the points (2, 3), (4, t) and (6, -3) are collinear, find the value of k using section formula.

Solution

Find the value of x and y so that the line through the pair of points has the given slope.

Problem 1 :

(x, 3) and (5, 9) and slope (m) = 2

Solution

Problem 2 :

(-2, 3) and (4, y) and slope (m) = -3

Solution

Problem 3 :

(-3, -5) and (4, y) and slope (m) = 3

Solution

Problem 4 :

(-8, -2) and (x, 2) and slope (m) = 1/2

Solution

Find a given that :

Problem 1 :

P(2, 3) and Q(a, -1) are 4 units apart

Solution

Problem 2 :

P(-1, 1) and Q(a, -2) are 5 units apart

Solution

Problem 3 :

X (a, a) is √8 units from the origin

Solution

Problem 4 :

A (0, a) is equidistant from P(3, -3) and  Q(-2, 2)

Solution

Problem 5 :

Find b given that A(3, -2) and B(b, 1) are √13 units apart.

Solution

Use the given distance d between the two points to find the value of x or y.

Problem 1 :

(0, 3), (x, 5); d = 2√10

Solution

Problem 2 :

(-3, -1), (2, y); d = √41

Solution

Problem 3 :

(x, 7), (-4, 1); d = 6√2

Solution

Problem 4 :

(1, y), (8, 13); d = √74

Solution

Problem 1 :

The point which lies on the perpendicular bisector of the line segment joining the points A(-2, -5) and B(2, 5) is

(A) (0, 0)    (B) (0, 2)    (C) (2, 0)    (D) (-2, 0)

Solution

Problem 2 :

The fourth vertex D of a parallelogram ABCD whose three vertices are A(-2, 3), B(6, 7) and C(8, 3) is

(A) (0, 1)    (B) (0, -1)    (C) (-1, 0)    (D) (1, 0)

Solution

Problem 3 :

If P(a/3, 4) is the midpoint of the line segment joining the points Q(-6, 5) and R(-2, 3), then the value of a is

(A) -4     (B) -12     (C) 12     (D) -6

Solution

Problem 4 :

The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at

(A) (0, 13)  (B) (0, -13)  (C) (0, 12)  (D) (13, 0)

Solution

Problem 5 :

The coordinates of the point which is equidistant from the three vertices of the Δ AOB.

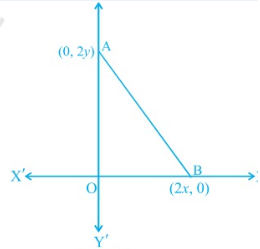
(A) (x, y)   (B) (y, x)   (C) x/2, y/2   (D) y/2, x/2

Solution

Problem 6 :

A circle drawn with origin as the center passes through (13/2, 0). The point which does not lie in the interior of the circle is

(A) (-3/4, 1)     (B) (2, 7/3)

(C) (5, -1/2)     (D) (-6, 5/2)

Solution

Problem 7 :

A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are respectively 

(A) (0, -5) and (2, 0)    (B) (0, 10) and (-4, 0)

(C) (0, 4) and (-10, 0)   (D) (0, -10) and (4, 0)

Solution

Problem 8 :

If the distance between the points (4, p) and (1, 0) is 5, then the value of p is

(A) 4 only     (B) ± 4     (C) -4 only     (D) 0

Solution