FIND MISSING ANGLES IN PARALLELOGRAM

Consecutive Angles in Parallelogram

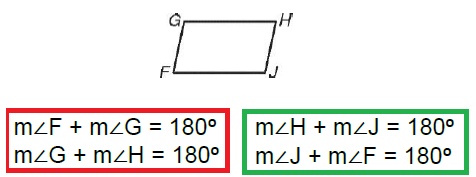
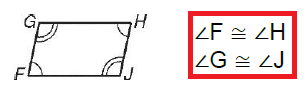
Opposite Angles in Parallelogram

Find the value of x that will make the shape a parallelogram and give a reason to support your answer.

Problem 1 :

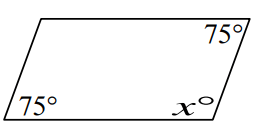
Solution :

Reason : Consecutive angles add upto 180.

75 + x = 180

x = 180 - 75

x = 105

Problem 2 :

Solve for x in the parallelogram given below.

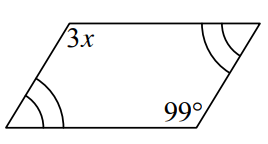
Solution :

Reason : Opposite angles are equal.

3x = 99

x = 99/3

x = 33

Problem 3 :

Solve for x in the parallelogram given below.

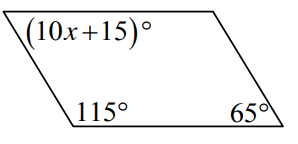
Solution :

Reason : Opposite angles are equal.

10x + 15 = 65

10x = 65 - 15

10x = 50

x = 50/10

x = 5

Problem 4 :

Solve for x and y in the parallelogram given below.

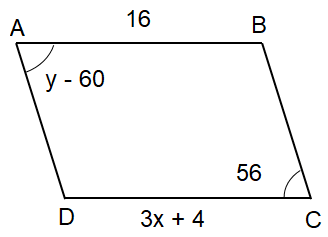
Solution :

Reason : Opposite angles are equal.

y - 60 = 56

y = 56 + 60

y = 116

Reason : Opposite sides are equal.

3x + 4 = 16

3x = 12

x = 12/3

x = 4

Problem 5 :

Use the diagram of parallelogram ABCD below to answer the questions.

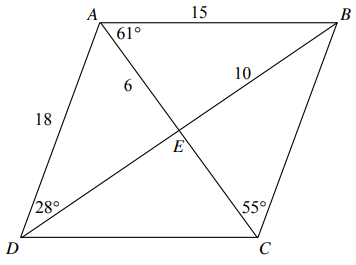
Solution :

1) CD = AB (Opposite sides)

CD = 15

2) ∠ADB = 28

3) ∠BDC :

In triangle ABC,

4) AC = 2AE ==> 2(6) ==> 12

5) ∠DCB = ∠DCA + ∠ACB

∠DCB = 61 + 55

∠DCB = 116

6) BE = 10

Problem 6 :

Solve for x and y in the parallelogram given below.

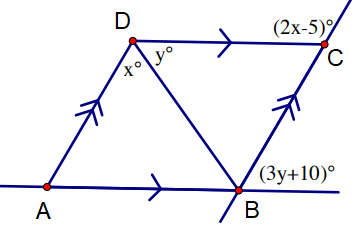
Solution :

AB and DC are parallel and DB is transversal.

∠DBC = x

In triangle DBC,

y + x = 2x - 5

x - 2x + y = -5

-x + y = -5  ------(1)

x + y + 3y + 10 = 180

x + 4y = 170  ------(2)

Problem 7 :

Find the missing value in each of the following parallelogram.

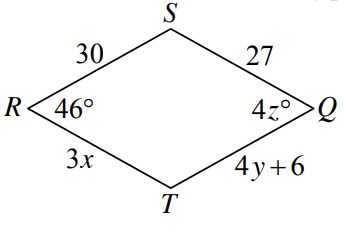
Solution :

Problem 8 :

Given that quadrilateral ABCD is a parallelogram find the values of x and y.

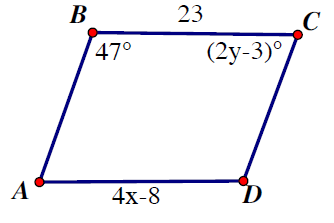
Solution :

Reasons : Sum of consecutive interior angles = 180

Opposite sides are equal.

Problem 9 :

Find the length of CF. AB = 12, AD = 10, CE = 8.

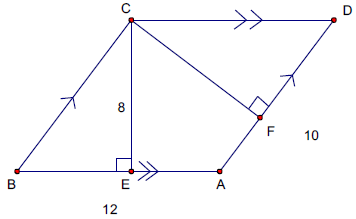
Solution :

In the parallelogram ABCD, CE and CF are perpendiculars.

Area of parallelogram = base x height

AB x CE = AD x CF

12 x 8 = 10 x CF

96 = 10 CF

CF = 96/10

CF = 9.6

Problem 10 :

Find the value of x that will make the shape a parallelogram  and give a reason to support your answer.

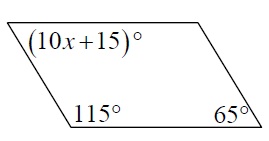
Solution :

Sum of consecutive interior angles = 180

10x + 15 + 115 = 180

10x + 130 = 180

10x = 180 - 130

10x = 50

x = 50/10

x = 5