FIND MISSING ANGLES IN ISOCELES TRAPEZIUM

What is Trapezium ?

A trapezium is a convex quadrilateral with exactly one pair of opposite sides parallel to each other. The trapezium is a two-dimensional are called legs. It is also called a trapezoid. Sometimes the parallelogram is also called a trapezoid with two parallel sides.

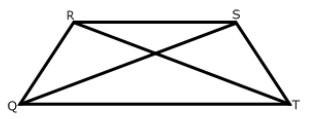
Properties :

(i)  All the properties of a trapezoid

(ii)  Non-parallel sides are congruent.

(iii)  Diagonals are congruent.

(iv)  Base angles are congruent.

(v)  Opposite angles are supplementary

Find the measurement of the angle indicated for each trapezoid.

Problem 1 :

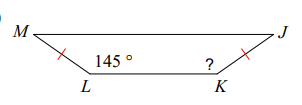
Solution :

∠MLK = 145°

Since the base angles are equal,

∠JKL = 145°

Problem 2 :

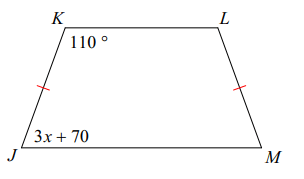
Solution :

The trapezium will have two parallel sides and two non parallel sides.

∠LKJ + ∠KJM = 180 (Co-interior angles)

110 + 3x + 70 = 180

180 + 3x = 180

3x = 180 - 180

3x = 0

x = 0/3

x = 0

Problem 3 :

Solution :

The trapezium will have two parallel sides and two non parallel sides.

∠MJK + ∠JKL = 180 (Co-interior angles)

6x + 6 + 120 = 180

6x + 126 = 180

Subtracting 126 on both sides.

6x = 180 - 126

6x = 54

Divide by 6 on both sides

x = 54/6

x = 9

Problem 4 :

Solution :

Opposite angles are supplementary.

14x + 11 + 85 = 180

14x + 96 = 180

14x = 180 - 96

14x = 84

Dividing by 14 on both sides.

x = 84/14

x = 6

Problem 5 :

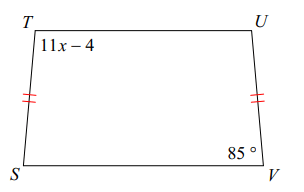
Solution :

Opposite angels are supplementary.

11x - 4 + 85 = 180

11x + 81 = 180

Subtracting 81, we get

11x = 180 - 81

11x = 99

Dividing by 11, we get

x = 99/11

x = 9

Problem 6 :

Given isosceles trapezoid 𝐴𝐵𝐶𝐷, 𝐵𝐶 ∥ 𝐴𝐷. If 𝑚 < 𝐴 = 3(2x − 7) and 𝑚 < 𝐶 = 4x + 1, find the value of x. Find the measure of all of the angles.

Solution :

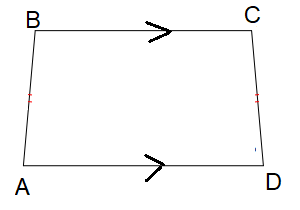
𝑚 ∠𝐴 = 3(2x − 7) and 𝑚 ∠𝐶 = 4x + 1

From the picture above, angle A and C are base angles and they are equal.

3(2x - 7) = 4x + 1

6x - 21 = 4x + 1

Subtracting 4x on both sides,

6x - 4x = 1 + 21

2x = 22

Dividing by 2 on both sides

x = 22/2

x = 11

Problem 7 :

Find ∠V

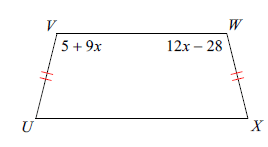
Solution :

Adjacent angels between parallel sides and one non parallel side add upto 180 degree.

5 + 9x = 12x - 28

Subtracting 12x and subtracting 5 on both sides.

9x - 12x = -28 - 5

-3x = -33

x = 33/3

x = 11

Angel V :

∠V = 5 + 9x

∠V = 5 + 9(11)

∠V = 5 + 99

∠V = 104

Problem 8 :

Find ∠M

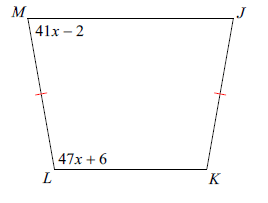
Solution :

Sum of co interior angles = 180

41x - 2 + 47x + 6 = 180

41x + 47x + 4 = 180

88x + 4 = 180

Subtracting 4 on both sides.

88x = 180 - 4

88x = 176

Dividing by 88, we get

x = 176/88

x = 2

∠M = 41x - 2

= 41(2) - 2

= 82 - 2 

∠M = 80

Problem 9 :

Isosceles trapezoid ABCD with BC ||AD. If m∠A = 4x+20 and m∠D = 2x+38, find m∠A, m∠B, m∠C, and m∠D.

Solution :

The base angles are equal

m∠A = 4x+20 and m∠D = 2x+38

m∠A = m∠D

4x + 20 = 2x + 38

4x - 2x = 38 - 20

2x = 18

x = 18/2

x = 9

Problem 10 :

In isosceles trapezoid ABCD, BC||AD. The measure of ∠ADC = 4x+20 and the measure of ∠DAB = 8x - 20. Find the value of x, ∠ADC, ∠DAB, ∠BCD, and ∠ABC.

Solution :

∠ADC = 4x+20 and ∠DAB = 8x - 20.

∠ADC = ∠DAB

4x + 20 = 8x - 20

4x - 8x = - 20 - 20

-4x = -40

x = 40/4

x = 10

∠BCD :

∠ADC and ∠BCD are co interior angles.

∠ADC + ∠BCD = 180

60 + ∠BCD = 180

∠BCD = 180 - 60

∠BCD = 120

∠DAB and ∠ABC are co interior angles.

∠DAB + ∠ABC = 180

60 + ∠ABC = 180

∠ABC = 180 - 60

∠ABC = 120