FIND MISSING ANGLES CREATED BY TANGENT LINES OF CIRCLE

Find the value of x in each diagram. The lines AB and AC are tangents.

Problem 1 :

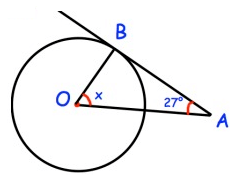
Solution :

∠BOA + ∠BAO + ∠OBA = 180^º

x + 27^º + 90^º = 180^º

x + 117^º = 180^º

x = 180^º - 117^º

x = 63^º

So, the value of x is 63^º.

Problem 2 :

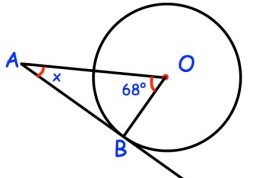
Solution :

∠BOA + ∠BAO + ∠OBA = 180^º

68^º + x + 90^º = 180^º

x + 158^º = 180^º

x = 180^º - 158^º

x = 22^º

So, the value of x is 22^º.

Problem 3 :

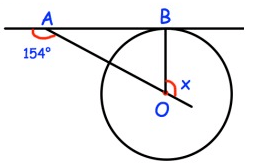
Solution :

154 + ∠OAB = 180

∠OAB = 180 - 154

∠OAB = 26

∠AOB + ∠OBA + ∠BAO = 180^º

x + 90 + 26 = 180

x + 116 = 180^º

x = 180^º - 116^º

x = 64^º

So, the value of x is 64^º.

Problem 4 :

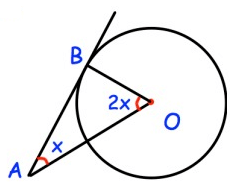
Solution :

Let ∠ABO

∠ABO + ∠BOA + ∠OAB = 180^º

90^º + 2x + x = 180^º

3x + 90^º = 180^º

3x = 180^º - 90^º

3x = 90^º

Dividing 3 on both sides.

3x/3 = 90^º/3

x = 30^º

So, the value of x is 30^º.

Problem 5 :

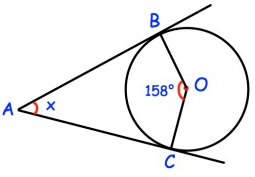
Solution :

In the quadrilateral ABOC,

∠BAC + ∠ACO + ∠COB + ∠OBA = 360

x + 90 + 158 + 90 = 360

x + 338 = 360

x = 360 - 338

x = 22

Problem 6 :

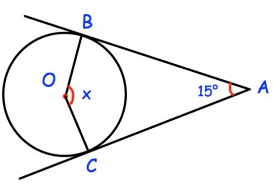
Solution :

In the quadrilateral ABOC,

∠BAC + ∠ACO + ∠COB + ∠OBA = 360

15 + 90 + x + 90 = 360

x + 195 = 360

x = 360 - 195

x = 165