FIND MAXIMUM MINIMUM VALUE AMPLITUDE FROM GRAPH OF PERIODIC FUNCTION

Find the maximum, minimum, and period of each periodic function. Then copy the graph and sketch two more cycles.

Problem 1 :

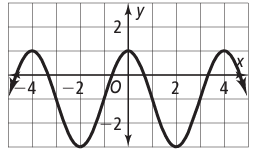
Solution :

Maximum = 1, minimum = -3

The horizontal length of the pattern = 4 units.

So, period = 4

Graph of two more cycles :

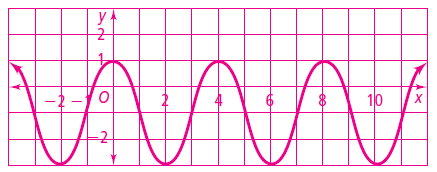
Problem 2 :

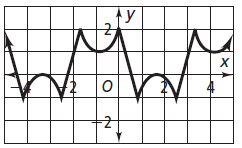
Solution :

Maximum = 2, minimum = -1

The horizontal length of the pattern = 5 units.

So, period = 5

Graph of two more cycles :

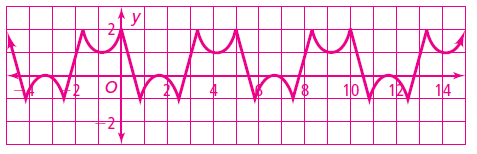
Find the maximum, minimum and amplitude of each periodic function.

Problem 3 :

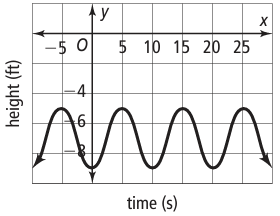
a. What is the period of the graph?

b. What is the amplitude of the graph?

Solution :

a)  The horizontal length of one pattern = 10 seconds. So, the period = 10.

b)  Amplitude = (Max - Min)/2

Maximum = -5, minimum = -9

= (-5 - (-9))/2

= (-5 + 9)/2

= 4/2

= 2

So, amplitude = 2

Find the maximum, minimum and amplitude of each periodic function.

Problem 4 :

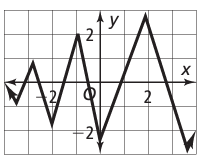
Solution :

The graph doesn't have pattern. So, it is not a periodic function.

Problem 5 :

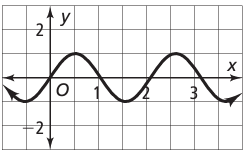
Solution :

It has a pattern, so it is a periodic function. The horizontal length of the pattern is 2 units. So, period is 2.

Maximum = 1, minimum = -1

 Amplitude = (Max - Min)/2

= (1 - (-1))/2

= (1+1)/2

= 2/2

= 1

So, amplitude = 1

Problem 6 :

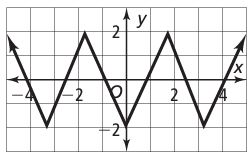
Solution :

It has a pattern, so it is a periodic function. The horizontal length of the pattern is 4 units. So, period is 4

Maximum = 2, minimum = -2

 Amplitude = (Max - Min)/2

= (2 - (-2))/2

= (2+2)/2

= 2

= 1

So, amplitude = 1