FIND LATERAL AND TOTAL SURFACE AREA OF CONE

What is cone ?

A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.

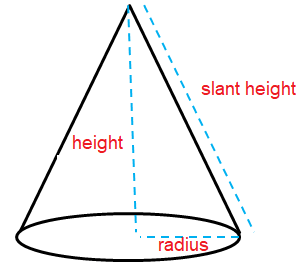
We can also define the cone as a pyramid which has a circular cross-section, unlike pyramid which has a triangular cross-section. These cones are also stated as a circular cone.

To find lateral surface area and total surface area of cone, we use the formulas given below.

Lateral surface area =  πrl

Total surface area =  πrl +  πr²

= πr(l + r)

l = √r² + h²

Here r = radius, l = slant height

Find 

(i) Lateral surface area

(ii)  Total surface area of the following cones given below.

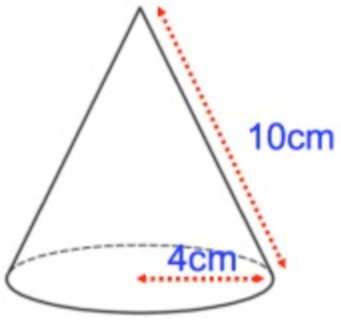
Problem 1 :

Solution :

(i)  Lateral surface area =  πrl

here radius (r) = 4 cm and slant height(l) = 10 cm

Lateral surface area = πrl

= π(4) (10)

= 40π cm²

(ii) Total surface area = πr(l + r)

= π(4)(10 + 4)

= 56π cm²

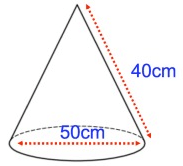
Problem 2 :

Solution :

(i)  Lateral surface area =  πrl

diameter = 50 cm, radius (r) = 25 cm, slant height (l) = 40 cm

= π(25) (40)

= 1000π cm²

(ii) Total surface area = πr(l + r)

= π(25)(40 + 25)

= 25π(65)

= 1625π cm²

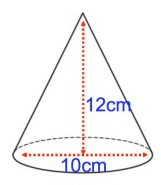
Problem 3 :

Solution :

(i)  Lateral surface area =  πrl

diameter = 10 cm, radius (r) = 5 cm, height (h) =  12 cm

l = √5² + 12²

l = √25 + 144

l = √169

l = 13 

= π(5) (13)

= 65π cm²

(ii) Total surface area = πr(l + r)

= π(5)(13 + 5)

= 5π(18)

= 90π cm²

Problem 4 :

The cone and cube below have the same surface areas. Workout the side length of cube x.

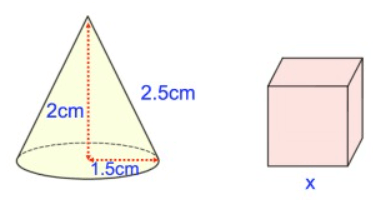
Solution :

Surface area of cone = surface area of cube

πrl = 4a²

From cone, r = 1.5 cm, h = 2 cm and l = 2.5 cm

π(1.5)(2.5) = 4x²

3.75π = 4x²

x² = 0.9375π

Here π = 3.14

x² = 0.9375(3.14)

x² = 2.94375

x = 1.71

Problem 5 :

A paper cup shaped like a cone and has a diameter of 6 cm and slant height of 7.5 cm. How much paper is need to make the cup ?

Solution :

Since the paper cup will be open at the bottom, it is enough to find paper used to cover lateral surface.

Quantity of paper required = πrl

r = 6/2 ==> 3 cm and slant height (l) = 7.5

= π(3) (7.5)

Here π = 3.14

= 3.14 (22.5)

= 70.65 cm²

Quantity of paper required is 70.65 cm².

Problem 6 :

The roof is shaped like a cone with the diameter of 12 feet. One bundle of shingles cover 32 square feet. How many bundles should you buy to cover the roof.

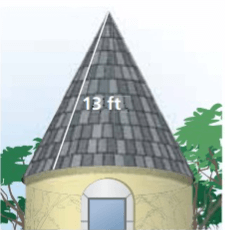
Solution :

Radius = 6 ft, slant height (l) = 13 ft

Area to be covered = πrl

= π(6) (13)

= 78π

Here π = 3.14

= 78(3.14)

= 244.92 ft²

One bundle of shingles cover 32 square feet

Number of shingles required = 244.92/32

= 7.65

So, approximately 8 bundles are needed.

Problem 7 :

Two Florida Atlantic University stickers are placed on opposite sides of megaphone. Estimate the percent of the surface area of the megaphone covered by the stickers. Round the answer to the nearest percent.

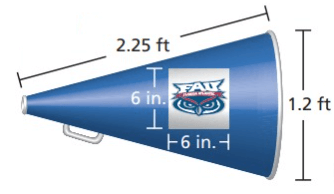
Solution :

Surface area of megaphone = πrl

r = 1.2/2 ==> 0.6 ft  ==>7.2 inches

l = 2.25 ft ==> 27 inches

Applying in the formula, we get

= 3.14 (7.2)(27)

= 610.416 square inches

Area of sticker = 6² ==>  36 square inches

Area of two stickers = 72 square inches

Area covered by two sticker in total area

= (72/610.416) x 100%

= 11.79

= 12%